SOLUTION: The length of the line segment joining X(square root 45, 2 square root 18) to the midpoint of Y(7 square root 5,-3 square root 2) and Z( square root5, -square root 2) is?

Algebra ->  Points-lines-and-rays -> SOLUTION: The length of the line segment joining X(square root 45, 2 square root 18) to the midpoint of Y(7 square root 5,-3 square root 2) and Z( square root5, -square root 2) is?      Log On


   

Question 180509: The length of the line segment joining X(square root 45, 2 square root 18) to the midpoint of Y(7 square root 5,-3 square root 2) and Z( square root5, -square root 2) is?
Answer by Fombitz(32388) About Me  (Show Source):
You can put this solution on YOUR website!
X=(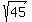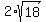sqrt%2845%29%29,+2%2Asqrt%2818%29)=(6.7,8.5)
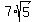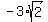Y=(7%2Asqrt%285%29+,+-3%2Asqrt%282%29+) =(15.7,-4.3)
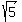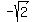Z=(sqrt%285%29+,+-sqrt%282%29+)=(2.2,-1.4)
Frist find the midpoint of YZ.
x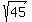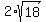%5Bm%5D=%28x%5BY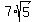%5D%2Bx%5BZ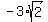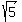%5D%29%2F2
x%5Bm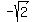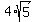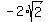%5D=%287%2Asqrt%285%29%2Bsqrt%285%29%29%2F2
x%5Bm%5D=%288%2Asqrt%285%29%29%2F2
x%5Bm%5D=4%2Asqrt%285%29
.
.
.
y%5Bm%5D=%28-3%2Asqrt%282%29%2B%28-sqrt%282%29%29%29%2F2
y%5Bm%5D=%28-4%2Asqrt%282%29%29%2F2
y%5Bm%5D=-2%2Asqrt%282%29
.
.
.
X=(sqrt%2845%29%29,+2%2Asqrt%2818%29)
Y=(7%2Asqrt%285%29+,+-3%2Asqrt%282%29+)
Z=(sqrt%285%29+,+-sqrt%282%29+)
M=(4%2Asqrt%285%29+,+-2%2Asqrt%282%29+)

Now use the distance formula,
D=sqrt%28%28x%5Bx%5D-x%5Bm%5D%29%5E2%2B%28y%5Bx%5D-y%5Bm%5D%29%5E2%29


D=sqrt%28%28-sqrt%285%29%29%5E2%2B%288%2Asqrt%282%29%29%5E2%29
D=sqrt%285%2B128%29
D=sqrt%28133%29