Question 163807: can you please help me solve these questions:-
1. "what is the equation of the circle who touches the negative x- and y-axes and also the line " "
2." what is the equation of the circle who passes through the points (1,4),(7,5),(1,8)?"
3."what is the equation of the circle who has its centre on the line  and passes through the origin and the point (4,2)?" and passes through the origin and the point (4,2)?"
Answer by Edwin McCravy(20059)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let's graph the line:
 We can draw two possible circles that touch that line and also the two
axes, a great big one and a tiny one:
We can draw two possible circles that touch that line and also the two
axes, a great big one and a tiny one:
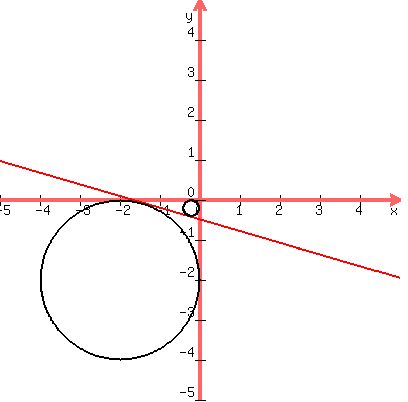 So we expect two solutions, both in quadrant 3.
Let the radius of the circle be r, In either case the circle's center
will then be (-r,-r).
If any circle with radius r in quadrant 3 touches both axes then
the points (-r,0) and (0,-r) are the points where the
circle touches the axes, and the circle has center (-r,-r), and
thus the equation of the circle is
So we expect two solutions, both in quadrant 3.
Let the radius of the circle be r, In either case the circle's center
will then be (-r,-r).
If any circle with radius r in quadrant 3 touches both axes then
the points (-r,0) and (0,-r) are the points where the
circle touches the axes, and the circle has center (-r,-r), and
thus the equation of the circle is
 This can be seen by drawing in these two radii,
since they are also the coordinates of the center (-r,-r)
(I'll just do it with the big circle.):
This can be seen by drawing in these two radii,
since they are also the coordinates of the center (-r,-r)
(I'll just do it with the big circle.):
 Now if we draw a third radius touching the line:
Now if we draw a third radius touching the line:
 We know that the distance from a point
We know that the distance from a point
 to a
line to a
line  is found by this equation: is found by this equation:
 So the distance from the line
So the distance from the line  to the center (-r,-r) must also be equal to the radius r,
of the circle
So substituting
to the center (-r,-r) must also be equal to the radius r,
of the circle
So substituting




 Squaring both sides
Squaring both sides





 Dividing through by 24
Dividing through by 24
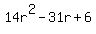

 So the big circle has radius 2 and its equation becomes
So the big circle has radius 2 and its equation becomes


 And the little circle has radius 3/14 and its equation becomes
And the little circle has radius 3/14 and its equation becomes


 --------------------------
2." what is the equation of the circle who passes
through the points (1,4),(7,5),(1,8)?"
Use the general equation of a circle:
--------------------------
2." what is the equation of the circle who passes
through the points (1,4),(7,5),(1,8)?"
Use the general equation of a circle:
 Substitute the point (x,y) = (1,4)
Substitute the point (x,y) = (1,4)



 Substitute the point (x,y) = (7,5)
Substitute the point (x,y) = (7,5)



 Substitute the point (x,y) = (1,8)
Substitute the point (x,y) = (1,8)



 Now we have a system of three equations in three
unknowns:
Now we have a system of three equations in three
unknowns:
 This has solution:
This has solution:
 So the equation of the circle:
So the equation of the circle:
 becomes becomes
 Multiplying through by 2:
Multiplying through by 2:
 -----------------------------------
3."what is the equation of the circle who has its centre
on the line
-----------------------------------
3."what is the equation of the circle who has its centre
on the line  and passes through the origin
and the point (4,2)?"
We'll draw the line and mark the point (4,2): and passes through the origin
and the point (4,2)?"
We'll draw the line and mark the point (4,2):
 Now since the circle must go through (0,0) and (4,2),
the line segment joining these two points must be a
chord of the circle. So we'll draw it.
Now since the circle must go through (0,0) and (4,2),
the line segment joining these two points must be a
chord of the circle. So we'll draw it.
 Now the perpendicular bisector of a chord must pass through
the center of the circle, so let's get the equation of the
perpendicular bisector of that chord from (0,0) to (4,2).
First we need its slope. So we find the slope of the chord,
take its reciprocal with the opposite sign.
Slope of the chord:
Now the perpendicular bisector of a chord must pass through
the center of the circle, so let's get the equation of the
perpendicular bisector of that chord from (0,0) to (4,2).
First we need its slope. So we find the slope of the chord,
take its reciprocal with the opposite sign.
Slope of the chord:



 So the slope of its perpendicular bisector is
So the slope of its perpendicular bisector is 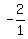 or or  .
The perpendicular bisector must also go through the midpoint of
the chord, so we use the midpoint formula: .
The perpendicular bisector must also go through the midpoint of
the chord, so we use the midpoint formula:


 So we find the equation of the perpendicular bisector of the
chord. It has slope = m =
So we find the equation of the perpendicular bisector of the
chord. It has slope = m =  and it goes through (2,1).
So we use the point-slope formula: and it goes through (2,1).
So we use the point-slope formula:



 So we'll draw this perpendicular bisector of the chord:
So we'll draw this perpendicular bisector of the chord:
 Where they intersect must be the center of the required
circle, so we solve the system of their equations:
Where they intersect must be the center of the required
circle, so we solve the system of their equations:
 Solving that system we get (x,y) = (4,-3).
So the center of the circle is (4,-3).
Solving that system we get (x,y) = (4,-3).
So the center of the circle is (4,-3).
 and we can sketch in the circle:
and we can sketch in the circle:
 We have its center (4,-3).
Now we must find its radius, which is the
distance from the center (4,-3) to the point (4,2).
We have its center (4,-3).
Now we must find its radius, which is the
distance from the center (4,-3) to the point (4,2).
 Using the distance formula:
Using the distance formula:





 So the radius is 5 and the center is (4,-3),
so the equation is
So the radius is 5 and the center is (4,-3),
so the equation is


 Edwin
Edwin
|
|
|