|
Question 161179: Write an equation of the line that passes through the point at (4,4) and is perpendicular to the line whose equation is 2x+y=7.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! Write an equation of the line that passes through the point at (4,4) and is perpendicular to the line whose equation is 2x+y=7.
since given line  which contains point ( which contains point ( , , ), we will find a line perpendicular to ), we will find a line perpendicular to  using what we know: using what we know:
 we can write in the slope-intercept form as we can write in the slope-intercept form as 
the slopes of the perpendicular lines are negative reciprocal; so the slope 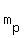 is negative reciprocal of the slope is negative reciprocal of the slope  from the line from the line , or , or 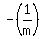
since  , the slope of the unknown line must be; , the slope of the unknown line must be;


we also know that line goes through ( , , ), and we can find the equation by plugging in this info into the ), and we can find the equation by plugging in this info into the 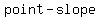 formula formula
Point-Slope Formula:
 where m is the slope and ( where m is the slope and ( , ,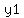 ) is the given point( ) is the given point( , , ) )
Plug in,  and and  , ,





Here is the graph:
 and and 
From the graph you can see that red line  contains point ( contains point ( , , ) )
| Solved by pluggable solver: Solve the System of Equations by Graphing |
Let's look at the first equation 
 Multiply both sides of the first equation by the LCD 2 Multiply both sides of the first equation by the LCD 2
 Distribute Distribute
---------
So our new system of equations is:


In order to graph these equations, we need to solve for y for each equation.
So let's solve for y on the first equation
 Start with the given equation Start with the given equation
 Add Add  to both sides to both sides
 Rearrange the equation Rearrange the equation
 Divide both sides by Divide both sides by 
 Break up the fraction Break up the fraction
 Reduce Reduce
Now lets graph  (note: if you need help with graphing, check out this solver) (note: if you need help with graphing, check out this solver)
 Graph of Graph of 
So let's solve for y on the second equation
 Start with the given equation Start with the given equation
 Subtract Subtract 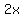 from both sides from both sides
 Rearrange the equation Rearrange the equation
 Divide both sides by Divide both sides by 
 Break up the fraction Break up the fraction
 Reduce Reduce
Now lets add the graph of  to our first plot to get: to our first plot to get:
 Graph of Graph of  (red) and (red) and  (green) (green)
From the graph, we can see that the two lines intersect at the point ( , , ) (note: you might have to adjust the window to see the intersection) ) (note: you might have to adjust the window to see the intersection) |
|
|
|
| |