SOLUTION: Find the equation of the circle described each. a)The circle is tangent to both coordinate axes and contains the point (6,3). b)The circle is circumscribed about the triangle

First plot the point (6,3)



I can see how there could be two different solutions, by drawing in
these:



The equation of a circle with center (h,k) and radius r is



Draw in radii to the axes:



We can see that since the circle has to be tangent to both axes, 
its center has to have the same x and y coordinates. and also that
the radius has to be equal to h as well.  So we can see that all
three values h, k, and r, must all be the same. So let them all be 
h, i.e., h = k = r, and we have



So since , we have


 


Now since it contains the point (6,3) we can substitute that in











That simplifies to



Factoring:



 or 
 or 

So we two values of , so

the two circles' equations are

 and 

 and 



b)The circle is circumscribed about the triangle whose vertices are (-1,-3),(-2,4),and (2,1). 

We plot the points:



We draw the triangle:



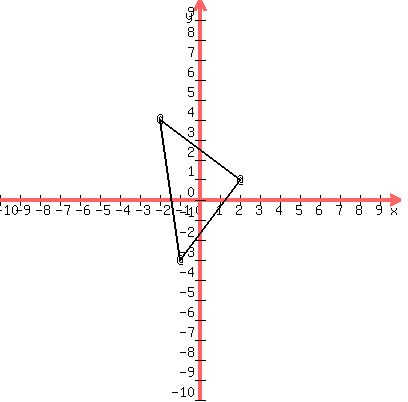The equation of a circle with center (,) and radius  is:



We substitute the point (,) = (,) 













Get all squared terms on right:



We substitute the point (,) = (,) 













Get all squared terms on right:



We substitute the point (,) = (,) 













Get all squared terms on right:



So we have the three equations:




 

Since the right sides of all three equations are equal,
then so are the left sides:



Using the first two





Using the first and third:





So we solve these two equations by 
substitution of elimination:




and get (h,k) = (,)

To find r we go back to



















Therefore the equation 



becomes





So we plot the center (,)



Now put the point of the compass on the center 
and draw the circle:



-----------------------

Maybe I'll do the last one tomorrow.  I'm getting sleepy. Check back to
see if I've done it.

Edwin