SOLUTION: Mr. Boone is a contractor who is building a house diagonally on a corner lot. To see if the house will fit where he wants it, he has drawn a blue print. The exterior walls of the

Algebra ->  Points-lines-and-rays -> SOLUTION: Mr. Boone is a contractor who is building a house diagonally on a corner lot. To see if the house will fit where he wants it, he has drawn a blue print. The exterior walls of the      Log On


   

Question 133222: Mr. Boone is a contractor who is building a house diagonally on a corner lot. To see if the house will fit where he wants it, he has drawn a blue print. The exterior walls of the house are perpendicular. He wants to know if he drew it correctly. Would the walls be perpendicular if the corners of the walls were at the coordinates (2,2), (4,3), (5,1), and (3,0)? Why?
Answer by vleith(2983) About Me  (Show Source):
You can put this solution on YOUR website!
Given points at (2,2), (4,3) (5,1) (3,0)
Are the lines that connect these points parallel and perpendicular? How doe sone know if one line is perpendicular to another? What does that say about their slopes?
segment from (4,3) to (2,2). slope is 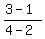%283-1%29%2F%284-2%29 = 1%2F2
segment from (3,0) to (5,1). slope is %281-0%29%2F%285-3%29 = 1%2F2 So these two segments are parallel since they have the same slope
segment from (4,3) to (5,1). slope is 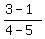%283-1%29%2F%284-5%29 = -2
segment from (2,2) to (3,0). slope is 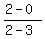%282-0%29%2F%282-3%29 = -2 these two are parallel since hey have the same slope
The slopes of the first set are the negative reciprocal of the second, so these lines are perpendicular.
The walls are perpendicular!