SOLUTION: Ace Carpentry needs to cut an arch for the top of an entranceway. The arch needs to be 8 ft. wide and 2 ft. high. To draw the arch, the carpenters will use a stretched string wit

Algebra ->  Circles -> SOLUTION: Ace Carpentry needs to cut an arch for the top of an entranceway. The arch needs to be 8 ft. wide and 2 ft. high. To draw the arch, the carpenters will use a stretched string wit      Log On


   

Question 123338This question is from textbook
: Ace Carpentry needs to cut an arch for the top of an entranceway. The arch needs to be 8 ft. wide and 2 ft. high. To draw the arch, the carpenters will use a stretched string with chalk attached at an end as a compass.
In the picture the top of the arch is point (0,2). The sides of the arch are (4,0) and (-4,0).
A) Using coordinate system, locate the center of the circle.
I tried to do the midpoint formula but couldn't figure the center using that and not with the distance, unless I am doing it all wrong.
B)What radius should the carpenters use to draw the arch?
 This question is from textbook

Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!





Discussion







This is a variation on the standard "given three non-collinear points,

determine the circle that intersects the the three points" problem.





The process involves several steps based on the geometric fact that the

perpendicular bisectors of all possible chords of a circle intersect in the

center of the circle.  A chord of a circle is a line segment that intersects

the circle in two places.





You need to determine the equations of the lines containing two chords, find

the mid-points of each chord, determine the equations of the perpendicular

bisectors of the two chords, and solve the system of equations represented by

the equations of the perpendicular bisectors.  That ordered pair solution will

be the circle center.





Equation of a line given two points:  y-y%5B1%5D=%28%28y%5B1%5D-y%5B2%5D%29%2F%28x%5B1%5D-x%5B2%5D%29%29%28x-x%5B1%5D%29





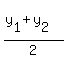Mid-point formula:  (%28x%5B1%5D%2Bx%5B2%5D%29%2F2,%28y%5B1%5D%2By%5B2%5D%29%2F2)





Equation of a line given the slope and one point:  y-y%5B1%5D=m%28x-x%5B1%5D%29





For part b of the problem, the distance formula applied to the circle center

and any one of the given points will give the radius.





The distance formula: d=sqrt%28%28x%5B1%5D-x%5B2%5D%29%5E2%2B%28y%5B1%5D-y%5B2%5D%29%5E2%29










Solution







First chord:  (4,0) to (0,2)

y-0=%28%280-2%29%2F%284-0%29%29%28x-4%29

y=-x%2F2%2B2



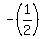
Slope is -%281%2F2%29



x-coordinate of mid-point:  %284%2B0%29%2F2=2

y-coordinate of mid-point:  %280%2B2%29%2F2=1





First chord mid-point is (2,1)





Equation of perpendicular bisector.  Slope of perpendicular:  -1%2F%28-%281%2F2%29%29=2.  Needs to contain point (2,1)



y-1=2%28x-2%29

y-1=2x-4

y=2x-3 is the equation of the first perpendicular bisector.





Second chord:  (-4,0) to (0,2)

y-0=%28%280-2%29%2F%28-4-0%29%29%28x%2B4%29

y=x%2F2%2B2



Slope is 1%2F2



x-coordinate of mid-point:  %28-4%2B0%29%2F2=-2

y-coordinate of mid-point:  %280%2B2%29%2F2=1





Second chord mid-point is (-2,1)





Equation of perpendicular bisector.  Slope of perpendicular:  -1%2F%281%2F2%29=-2.  Needs to contain point (-2,1)



y-1=-2%28x%2B2%29

y-1=-2x-4

y=-2x-3 is the equation of the second perpendicular bisector.





System of equations:

y=2x-3 1st perpendicular bisector

y=-2x-3 2nd perpendicular bisector





Add the equations:

2y=0x-6

y=-3





-3=2x-3

2x=0

x=0





So the circle center is at (0,-3)





Problem part b:

Calculate the distance from (0,2) to (0,-3).  Since both of these points lie

on the y-axis, you can just subtract the two y-coordinates to determine the

distance representing the radius of the circle:  2-%28-3%29=5.  But in

general, you would use the distance formula:





d=sqrt%28%280-0%29%5E2%2B%282-%28-3%29%29%5E2%29

d=sqrt%285%5E2%29=5