Question 1209524: (46) Sector ABC is 1/12 of a circle with diameter 24k. Line segment AD is perpendicular to segment BC. Find the area of the shaded region.
Link to diagram: https://ibb.co/5gNwX0K6
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website! Let's break the problem down step by step:
### **Step 1: Determine the Radius of the Circle**
- The given diameter of the circle is \( 24k \), so the radius is:
\[
r = \frac{24k}{2} = 12k
\]
### **Step 2: Compute the Area of Sector ABC**
- The full circle has an area of:
\[
A_{\text{circle}} = \pi r^2 = \pi (12k)^2 = 144\pi k^2
\]
- Since sector ABC is \( \frac{1}{12} \) of the full circle, its area is:
\[
A_{\text{sector}} = \frac{1}{12} \times 144\pi k^2 = 12\pi k^2
\]
### **Step 3: Find the Area of Triangle ABD**
- Since \( AD \) is perpendicular to \( BC \), we assume \( AD \) is the height of \( \triangle ABC \), where \( BC \) is the chord of the sector.
- The central angle of the sector is:
\[
\theta = \frac{360^\circ}{12} = 30^\circ
\]
- The triangle \( \triangle ABC \) is an isosceles triangle with two equal sides being the radii \( 12k \), and the included angle \( 30^\circ \).
- Using the formula for the area of a triangle:
\[
A_{\triangle ABC} = \frac{1}{2} r^2 \sin \theta
\]
\[
= \frac{1}{2} (12k)^2 \sin 30^\circ
\]
\[
= \frac{1}{2} (144k^2) \times \frac{1}{2}
\]
\[
= \frac{144k^2}{4} = 36k^2
\]
### **Step 4: Compute the Shaded Region**
- The shaded area is the sector minus the triangle:
\[
A_{\text{shaded}} = A_{\text{sector}} - A_{\triangle ABC}
\]
\[
= 12\pi k^2 - 36k^2
\]
\[
= 36k^2 (\pi - 1)
\]
Thus, the area of the shaded region is:
\[
\boxed{36k^2 (\pi - 1)}
\]
Answer by ikleyn(52817)  (Show Source):
You can put this solution on YOUR website! .
Sector ABC is 1/12 of a circle with diameter 24k. Line segment AD is perpendicular to segment BC.
Find the area of the shaded region.
Link to diagram: https://ibb.co/5gNwX0K6
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution in the post by @CPhill is INCORRECT.
I came to bring a correct solution.
We should take the area of the sector ABC and subtract from it the area of triangle ABD.
The area of the sector ABC is 1/12 of the area of the circle
area of the sector ABC is  =  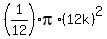=  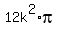. (1)
Triangle ABD has the angle B = 30°.
So, its leg AD is 12k/2 = 6k long;
leg BD is  .
The area of triangle ABD is half the product of the legs
area ABD = 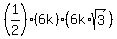 =  . (2)
Thus the area of the shaded region is the difference (1) minus (2)
area of the shaded region is  =  ,
or approximately  =  .
Solved.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Regarding the post by @CPhill . . .
Keep in mind that @CPhill is a pseudonym for the Google artificial intelligence.
The artificial intelligence is like a baby now. It is in the experimental stage
of development and can make mistakes and produce nonsense without any embarrassment.
It has no feeling of shame - it is shameless.
This time, again, it made an error.
Although the @CPhill' solution are copy-paste Google AI solutions, there is one essential difference.
Every time, Google AI makes a note at the end of its solutions that Google AI is experimental
and can make errors/mistakes.
All @CPhill' solutions are copy-paste of Google AI solutions, with one difference:
@PChill never makes this notice and never says that his solutions are copy-past that of Google.
So, he NEVER SAYS TRUTH.
Every time, @CPhill embarrassed to tell the truth.
But I am not embarrassing to tell the truth, as it is my duty at this forum.
And the last my comment.
When you obtain such posts from @CPhill, remember, that NOBODY is responsible for their correctness,
until the specialists and experts will check and confirm their correctness.
Without it, their reliability is ZERO and their creadability is ZERO, too.
. . . . . . . . . . . . . . . . . . . . . . . .
I reviewed many geometric problems, where @CPhill (= artificial intelligence) produced wrong solutions.
My resume from my reviews to these solutions is that this AI in its current version
is MENTALLY BLIND regarding Geometry problems.
|
|
|
