Question 1208994: An archery target is constructed of five concentric circles such that the area of the inner circle is equal to the area of each of the four rings. If the radius of the outer circle is 12 m, then the width of band a, in m.
https://ibb.co/h78NMWQ
I am very confused as to which band is a and what method to use for this
Answer by ikleyn(52914)   (Show Source): (Show Source):
You can put this solution on YOUR website! An archery target is constructed of five concentric circles such that the area of the inner circle
is equal to the area of each of the four rings. If the radius of the outer circle is 12 m, then
 the width of band a, in m. the width of band a, in m.
https://ibb.co/h78NMWQ
I am very confused as to which band is a and what method to use for this
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
We have one circle and four rings: in all, 1 + 4 = 5 shapes of equal areas.
The area of the outer circle is  = =  .
The area of each shape is 1/5 of the total area,
since the partial areas of all shapes are equal to each other.
They want you find the width of the band for the ring between the third and the second circles
(counting from the center).
For the area of the second circle you have .
The area of each shape is 1/5 of the total area,
since the partial areas of all shapes are equal to each other.
They want you find the width of the band for the ring between the third and the second circles
(counting from the center).
For the area of the second circle you have
 = =  ,
where ,
where  is the radius of the second circle. So, from this equation is the radius of the second circle. So, from this equation
 = =  , ,
 = =  = =  meters.
For the area of the third circle you have meters.
For the area of the third circle you have
 = =  ,
where ,
where  is the radius of the third circle. So, from this equation is the radius of the third circle. So, from this equation
 = = 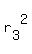 , ,
 = =  = =  meters.
Now the width of the band " a " is the difference
a = meters.
Now the width of the band " a " is the difference
a =  - -  = = 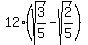 = 1.70569 meters (rounded). = 1.70569 meters (rounded).
It is your answer, and at this point the problem is solved in full, i.e. completely.
|
|
|