SOLUTION: The general form of an equation of a circle is given. Convert to the standard form. 2x^2 + 2y^2 + 8x + 7 = 0 Let me see. 2x^2 + 8x + 2y^2 = (-7)^2 2(x^2 + 4x)

Click here to see ALL problems on Circles

Question 1207930: The general form of an equation of a circle is given. Convert to the standard form.

2x^2 + 2y^2 + 8x + 7 = 0

Let me see.

2x^2 + 8x + 2y^2 = (-7)^2

2(x^2 + 4x) + y^2 = 49

2(x^2 + 4x + 4) + y^2 = 49

2(x + 2)(x + 2) + y^2 = 49

2(x + 2)^2 + y^2 = 49

Is this right?

Found 5 solutions by josgarithmetic, ikleyn, greenestamps, math_tutor2020, MathTherapy:
Answer by josgarithmetic(39620)   (Show Source):
You can put this solution on YOUR website!

the x-parts need some work. The y-parts are fine.
Completing The Square requires 4.

------------You take it from here!

Answer by ikleyn(52803)   (Show Source):
You can put this solution on YOUR website!
.

The general form of an equation of a circle is given. Convert to the standard form. 2x^2 + 2y^2 + 8x + 7 = 0 Let me see. 2x^2 + 8x + 2y^2 = (-7)^2 <<<---=== (-7)^2 in the right side is a mistake 2(x^2 + 4x) + y^2 = 49 <<<---=== the coefficient "2" at y^2 is missed. 2(x^2 + 4x + 4) + y^2 = 49 2(x + 2)(x + 2) + y^2 = 49 2(x + 2)^2 + y^2 = 49 Is this right?
--------------------

It is wrong. I marked the lines where you made mistakes.

So, you should redo it, fixing these mistakes.

Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!

Your question is "Is this right?"

The answer is "NO".

It can't be right. In the given form, the coefficients of x^2 and y^2 are equal, which makes the equation an equation of a circle.

In your final equation, the coefficients of x^2 and y^2 are not equal.

So look at your own work and find where the coefficients of x^2 and y^2 become unequal. That will show you where you made an error in your work.

Then go back and fix that error to finish solving the problem correctly.

Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!

I appreciate you showing your steps and thought process.

The first mistake happens when you go from
2x^2 + 2y^2 + 8x + 7 = 0
to
2x^2 + 8x + 2y^2 = (-7)^2
I'm not sure why you are squaring that -7.

Instead it should be
2x^2 + 2y^2 + 8x + 7 = 0
to
2x^2 + 2y^2 + 8x = -7

Another mistake you made is the portion going from x^2+4x to x^2+4x+4
Those two expressions are not the same thing.
What you'll need to do is add and subtract 4 to keep things balanced.
x^2+4x = x^2+4x+4-4 = (x^2+4x+4) - 4 = (x+2)^2-4
The stuff in red represents adding 0, which doesn't change the expression.

--------------------------------------------------------------------------

Here is how I would tackle this problem.

2x^2 + 2y^2 + 8x + 7 = 0
(2x^2 + 8x) + 2y^2 + 7 = 0
2(x^2 + 4x) + 2y^2 + 7 = 0
2(x^2 + 4x +0) + 2y^2 + 7 = 0
2(x^2 + 4x +4-4) + 2y^2 + 7 = 0
2( (x^2+4x+4) - 4 ) + 2y^2 + 7 = 0
2( (x+2)^2 - 4 ) + 2y^2 + 7 = 0
2(x+2)^2 - 8 + 2y^2 + 7 = 0
2(x+2)^2 + 2y^2 -1 = 0
2(x+2)^2 + 2y^2 = 1
(x+2)^2 + y^2 = 1/2 this is the equation in standard form.

The standard form template of a circle is
(x-h)^2 + (y-k)^2 = r^2
Compare that template to the stuff in red to see the center is located at (h,k) = (-2,0)
It might help to rewrite (x+2)^2 as (x-(-2))^2
It might help to rewrite y^2 as (y-0)^2
These rewrites aren't necessary if you can spot the h,k values easily at this point.

Now compare the right hand sides to find the radius.
r^2 = 1/2
r = sqrt(1/2) = 1/sqrt(2) = sqrt(2)/2
There are a few ways to represent the radius.
All of which approximate to roughly 0.70710678

I used GeoGebra to confirm the answer is correct.
Desmos is another good option.

Answer by MathTherapy(10552)   (Show Source):
You can put this solution on YOUR website!

The general form of an equation of a circle is given. Convert to the standard form. 2x^2 + 2y^2 + 8x + 7 = 0 Let me see. 2x^2 + 8x + 2y^2 = (-7)^2 2(x^2 + 4x) + y^2 = 49 2(x^2 + 4x + 4) + y^2 = 49 2(x + 2)(x + 2) + y^2 = 49 2(x + 2)^2 + y^2 = 49 Is this right? As stated by others, your approach is WRONG. Correct way to do this is: Standard form of the equation of a circle: , where: is a point on the circle's circumference 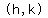is the CENTER of the circle is the circle's RADIUS To convert to STANDARD FORM, we need to COMPLETE the "SQUARES," as follows: ---- Placing the variables in order, and moving the CONSTANT to the right side --- Dividing EACH SIDE by 2, in order to get "+ 1" on the variables' SQUARES (x² and y²) ---- Taking of b, on x, and of b, on y, and then SQUARING THEM ---- Adding "+ 2²" and 0² to both sides of the equation <=== Standard form of circular-equation, 2x² + 2y² + 8x + 7 = 0 (general-form).