SOLUTION: Given the two circles defined by the equations x^(2)-6x+y^(2)+8y=12 and x^(2)+y^(2)=4y, find the algebraic equation of the line connecting their centers.

Algebra ->  Points-lines-and-rays -> SOLUTION: Given the two circles defined by the equations x^(2)-6x+y^(2)+8y=12 and x^(2)+y^(2)=4y, find the algebraic equation of the line connecting their centers.      Log On


   

Question 1206482: Given the two circles defined by the equations x^(2)-6x+y^(2)+8y=12 and x^(2)+y^(2)=4y, find the algebraic equation of the line connecting their centers.
Found 3 solutions by ikleyn, math_tutor2020, greenestamps:
Answer by ikleyn(52915) About Me  (Show Source):
You can put this solution on YOUR website!
.
Given the two circles defined by the equations x^(2)-6x+y^(2)+8y=12 and x^(2)+y^(2)=4y,
find the algebraic equation of the line connecting their centers.
~~~~~~~~~~~~~~~~~~~ 

To find the centers, apply completing the squares separately to x-terms and y-terms in each equation.


                It can be done MENTALLY.


The center of the 1st circle is the point (3,-4).

The center of the 2nd circle is the point (0,2).


The slope of the line through the centers is  m = 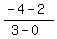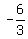%28-4-2%29%2F%283-0%29 = -6%2F3 = -2.


So, an equation of the line can be presented in the form

    y-2 = m*(x-0),

or

    y - 2 = -2x,  or  y = -2x + 2,


or in any other equivalent form.


You can check on your own that the presented equations are satisfied with
the coordinates of the centers, so this straight line goes through these points.

Solved.



Answer by math_tutor2020(3817) About Me  (Show Source):
You can put this solution on YOUR website!

Answer: y = -2x+2

Explanation

Let's complete the square for the 1st equation.
x^2-6x+y^2+8y = 12
(x^2-6x)+(y^2+8y) = 12
(x^2-6x+9-9)+(y^2+8y+16-16) = 12
(x^2-6x+9)+(y^2+8y+16)-9-16 = 12
(x-3)^2+(y+4)^2-25 = 12
(x-3)^2+(y+4)^2 = 12+25
(x-3)^2+(y+4)^2 = 37
This circle is centered at (h,k) = (3,-4)
The radius is r = sqrt(37)
The circle template is (x-h)^2+(y-k)^2 = r^2
On the 3rd step, I added and subtracted 9 in the first parenthesis grouping. This is to complete the square for the x terms. I took half of the x coefficient and squared it.
The same idea is used to complete the square for the y terms also.

Now complete the square for the other equation.
x^2+y^2 = 4y
x^2+y^2-4y = 0
x^2+( y^2-4y ) = 0
x^2+( y^2-4y + 4-4) = 0
x^2+( y^2-4y + 4) -4 = 0
x^2+(y-2)^2 -4 = 0
x^2+(y-2)^2 = 4
(x-0)^2+(y-2)^2 = 4
The center here is (0,2). The radius is 2.
On the 4th step, I took half of the y coefficient and squared it. That explains the +4-4 part at the end of the parenthesis grouping.

The two centers we found were
A = (3,-4)
B = (0,2)

Let's find the equation of line AB.
First we need the slope.


m+=+%28y%5B2%5D+-+y%5B1%5D%29%2F%28x%5B2%5D+-+x%5B1%5D%29
m+=+%282+-+%28-4%29%29%2F%280+-+3%29
m+=+%282+%2B+4%29%2F%280+-+3%29
m+=+%286%29%2F%28-3%29
m+=+-2
The slope of line AB is m = -2.

The y intercept is b = 2 due to the point (0,2).

The equation of line AB is therefore y = -2x+2 since the slope-intercept template is y = mx+b.

You can use a tool like GeoGebra to confirm the answer.

Answer by greenestamps(13216) About Me  (Show Source):
You can put this solution on YOUR website!


If you need to find the centers and radii of the two circles, then you need to complete the squares.

In this problem, you are to find the equation of the line connecting the centers of the circles. That means you don't need to know the radii of the two circles; and that means completing the square is unnecessary work.

As tutor @ikleyn says, you can find the centers of the two circles mentally:

First circle: (x^2-6x+...)+(y^2+8y+...) = ... ---> center (3,-4)
Second circle: (x^2)+(y^2-4y+...) = ... ---> center (0,2)

Then finding the equation of the line containing those two centers is a basic algebraic process.