SOLUTION: This question below is part 2 of a question I had recently posted on algebra.com ( please see the previous question here on algebra.com about average rate of change (https://www.al

Click here to see ALL problems on Miscellaneous Word Problems

Question 1203202: This question below is part 2 of a question I had recently posted on algebra.com ( please see the previous question here on algebra.com about average rate of change (https://www.algebra.com/my/your-answer.mpl?question=1203157)

image upload

A request: I haven't learned to solve this using derivatives so please solve using another method ( I use a different formula that doesn't require derivatives)

Thank you in advance!

Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817) (Show Source):
You can put this solution on YOUR website!

I'll use x in place of theta
And use y in place of T

Here are two resources to check out
https://math.libretexts.org/Bookshelves/Calculus/Calculus_(OpenStax)/03%3A_Derivatives/3.05%3A_Derivatives_of_Trigonometric_Functions
and
https://math.libretexts.org/Courses/Mount_Royal_University/MATH_1200%3A_Calculus_for_Scientists_I/1%3A_Limit__and_Continuity_of_Functions/1.7%3A_Limit_of__Trigonometric_functions

The first link talks about the derivative of trig functions.
What we're interested in mainly is that
derivative of sine = cosine
or in terms of symbols
d/dx[ sin(x) ] = cos(x)

Rephrased another way
y = sin(x) leads to dy/dx = cos(x)

The second link is a supplement to explain two important trig limit identities.

If y = (2V/g)*sin(x) then dy/dx = (2V/g)*cos(x)
The (2V/g) portion is a constant.

Plug in x = pi/6 to get:
dy/dx = (2V/g)*cos(x)
dy/dx = (2V/g)*cos(pi/6)
dy/dx = (2V/g)*sqrt(3)/2
dy/dx = (V/g)*sqrt(3)

Use the unit circle to determine that cos(pi/6) = sqrt(3)/2

Answer: The instantaneous rate of change is (V/g)*sqrt(3) when theta = pi/6

-------------------

Edit:

I just realized you wrote that you haven't learned derivatives just yet.
Another approach would be to find the average rate of change over the interval [pi/6, pi/4] as done so in this link
https://www.algebra.com/algebra/homework/word/misc/Miscellaneous_Word_Problems.faq.question.1203157.html

pi/6 = 0.523599 approximately
pi/4 = 0.785398 approximately

So the interval [pi/6, pi/4] is approximately [0.523599, 0.785398]

Then shrink that interval down to something like [0.523599, 0.7] then to [0.523599, 0.6]
The idea is to keep shrinking the interval such that pi/6 = 0.523599 is kept constant as the left endpoint. Only the right endpoint will move closer and closer to pi/6

As this right side approaches pi/6, the average rate of change will approach the instantaneous rate of change.

Answer by ikleyn(52794) (Show Source):
You can put this solution on YOUR website!
.

As I read this assignment, I am perplexed.

I am perplexed, because I do not understand its meaning.

I do not understand its meaning, because I do not understand, which instantaneous velocity is under the question.

Behind these words "instantaneous velocity", two different notions/conceptions are nested.

One conception is the instantaneous velocity of the baseball of the problem 1203157-(#1),
which is hit at initial velocity V and angle = to the horizon.

Another conception is the instantaneous "rate of change" of the function 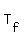of the problem 1203157-(#1);
but in this case the right name for this conception is the "instantaneous rate of change" - - - not the "instantaneous velocity".

So, in my view, the assignment is written carelessly.
I would even say, defiantly and provocatively carelessly.
In such situation, I prefer do not touch the problem.

It is just enough to explain why the problem is defective.

====================

I got this message (as a comment) from you: Hello ikleyn, There is a continuation to Question 1203157
which you were so helpful in solving. The second part of the question asks :
Find the instantaneous velocity at thita = pi/6 for problem # 1 ( which you solved previously - Question 1203157)
Should I post this again on algebra.com

My response: every new problem must be submitted to www.algebra.com.

It is a UNIQUE way to submit a problem.

Submitting to personal page is PROHIBITED, because in this case I DO NOT KNOW to whom to answer.

Again: every new problem must be submitted to www.algebra.com.
It is a UNIQUE way to submit a problem.
Submitting to personal page is PROHIBITED, because in this case I DO NOT KNOW to whom to answer.

////////////////////

I just got one more your comment:

Comment from student: Hello , it is word for word from my assignment.
I can send you a picture of both questions together if you prefer.

My response: Please, I want you understand me in a right way.

I do not state that it is you are a person who messed up the problem.

It is a person who created it - the Math composer.

For me, it does not matter who is guilty personally.

For me, the only fact which matters is that the problem is defective.

Regarding you PERSONALLY, I only can say, based on your last comment,
that you blindly copy-paste the text, without thinking on its meaning, unfortunately.

I see such situation at this forum several times per day, every day.

As a consolation, you, probably, have a professor or a teacher
or a supervisor to ask for and to clarify the question.