SOLUTION: A unit circle has its center at (5,0) and a second circle with a radius of 2 units has its center at (11,0) as shown. A common internal tangent to the circles intersects the x-axis

Let A = (5,0) and E = (11,0)  be the centers of the circles;

let B and D be the tangent points on greater and smaller circles, respectively;

Q = (a,0) is the intersection point of the common internal tangent to the circles
with the x-axis.


Draw the radii AB and ED to tangent points and consider triangles ABQ and QDE.

These triangles are right-angled triangles with right angles at the tangent points B and D.
They have congruent acute angles at the intersection point Q.
Hence, these triangles are similar.


Their corresponding sides are the radii AB = 1 and ED = 2 (the legs).
Their other corresponding sides are AQ and EQ (the hypotenuses),
so we can write 

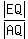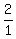     =  = 2.


From the other side,  AQ + EQ = AE = 11 - 5 = 6 units.


So, the intersection point Q divides the segment AE of the length 6 units 
in segments  EQ  and  AQ  in proportion  2:1.

It implies that  AQ  is one third of  AE=6;  in other words,  AQ = 2 units.


Hence, the value "a" under the problem's question is  a = 5 + 2 = 7 units.    ANSWER