|
Question 1200535: The line x - 2y + 4 = 0 is tangent to a circle at (0,2). The line y = 2x - 7 is tangent to the same circle at (3, -1). Find the center of the circle.
NOTE: I WORKED THIS OUT WRONGLY ON PAPER. I DON'T KNOW HOW TO UPLOAD PHOTOS ON THIS MATH SITE WHICH IS VERY LIMITED.
Found 3 solutions by Alan3354, math_tutor2020, ikleyn:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! The line x - 2y + 4 = 0 is tangent to a circle at (0,2). The line y = 2x - 7 is tangent to the same circle at (3, -1). Find the center of the circle.
------------
Find the slope of each line.
Then find the slope of the lines thru the points and perpendicular to the given lines.
Then find the equations of the perpendicular lines.
Find the intersection of the lines.
That's the center of the circle (point (h.k)).
----
========================================
Not requested:
---
The distance from the center of the circle to either given point is the radius of the circle, r.
-------
The equation of the circle is (x-h)^2 + (y-k)^2 = r^2
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
To share images, upload them to a website like Imgur (or similar).
After it's uploaded to that website, you can share the link.
Let's solve for y in the first equation
x - 2y + 4 = 0
-2y = -x-4
y = (-x-4)/(-2)
y = (1/2)x + 2
This equation has a slope of 1/2
The negative reciprocal of 1/2 is -2/1 aka -2
Therefore, the equation perpendicular to x - 2y + 4 = 0 will have a slope of -2.
Why are we looking for a perpendicular line? Because the tangent line is perpendicular to the radius when meeting at the point of tangency. Check out the diagram below.
We'll use this perpendicular slope and the coordinates (x,y) = (0,2) to determine the equation of the perpendicular line is y = -2x+2
Another approach you can take is outlined in this lesson
https://www.algebra.com/algebra/homework/Linear-equations/perpendicular-line-example1.lesson
Through similar steps, the perpendicular line to y = 2x-7 that passes through (3,-1) is y = (-1/2)x + 1/2
--------------------------------------------------
The two perpendicular lines we found
y = -2x+2
y = (-1/2)x + 1/2
will have the circle diameters located on them.
As such, those lines intersect to pinpoint the center of the circle.
y = (-1/2)x + 1/2
-2x+2 = (-1/2)x + 1/2
2*(-2x+2) = 2*((-1/2)x + 1/2)
-4x+4 = -x+1
-4x+x = 1-4
-3x = -3
x = -3/(-3)
x = 1
Then,
y = -2x+2
y = -2*1+2
y = 0
The center is located at (x,y) = (1,0)
So we know that (h,k) = (1,0)
i.e. we have h = 1 and k = 0
Those h and k values are useful for the circle template
(x-h)^2 + (y-k)^2 = r^2
Diagram

I used GeoGebra, but Desmos is another good option.
--------------------------------------------------
--------------------------------------------------
Answer: Center is (1,0)
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
This problem has an underwater stone, which is usually unseen to many people.
This underwater stone is that the problem is OVER-defined.
Indeed, the condition giving coordinates of TWO tangent points is EXCESSIVE:
one tangent point is just enough and it defines the second tangent point
by an UNIQUE way.
In couple of words, I will explain WHY the problem is over-defined.
Indeed, we know that the center must lie on the bisector of the angle,
concluded by the given lines.
From the other side, the center of the circle must lie on the perpendicular
to one of the given lines at the tangency point - so the center
of the circle is the intersection of the angle bisector and the
perpendicular to one of the tangency line at the tangency point.
What are the consequences from the fact that the problem is over-defined ?
The consequence is that when the center is found as the intersection point
of two perpendiculars to the given lines at the tangency points,
the person, who solves the problem, MUST check that the distance
from the intersection point to the given tangency points IS THE SAME:
It will guarantee that the condition of the problem
is self-consistent and is not self-contradictory.
Without such a check, the solution is formally incomplete;
it is completed ONLY when the check is done.
Fortunately, in our case (it is easy to check) the distance from the intersection
point (1,0) to the given tangency points is the same: it is equal to  . .
--------------------
Comment from student : It's easier of the author provided a graph.
My response : In Geometry, the plots are never considered as a proof
or a tool to make a proof: the plots work and are used for visualization, ONLY.
Especially, in this problem, where the radius is an irrational number  , ,
and you can not distinct visually  from from 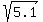 . .
So, your attempt to object or to argue my conception is invalid.
|
|
|
| |