|
Question 1197251: find the interior angles of the triangle whose vertices are (-3,3), (-1,-1), (3,-3)
Found 3 solutions by Alan3354, ewatrrr, math_tutor2020:
Answer by Alan3354(69443)   (Show Source): (Show Source):
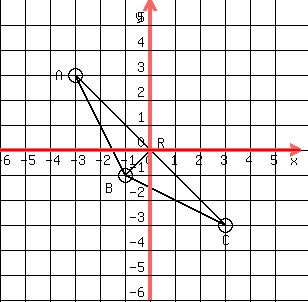
You can put this solution on YOUR website! find the interior angles of the triangle whose vertices are A(-3,3), B(-1,-1), C(3,-3)
---------------------------
The slope of BC is zero (0).
The slope of AB is -4/2 = -2
The slope of AC is 6/-6 = -1
--------------------
atan(-1) = 135 degs with the x-axis ---> interior angle of 45 degs at point C.
atan(-2) = ~ -63.435 degs --> interior angle of 116.565 degs
The 3rd angle = 180 - the sum of the other 2.
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website! Using the right triangle formed: Slope AC = -1, Slope BR = 1
BR = √2, RC = AR =√18 , BC = AB = √20 , Triangles congruent
∠A = ∠C = 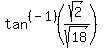 ~ 18.435° ~ 18.435°
∠B = 180 - 2*18.435
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A = (-3,3)
B = (-1,-1)
C = (3,-3)
Use the distance formula to calculate the distance from A to B, which gives the length of side AB.
(x1,y1) = (-3,3) and (x2, y2) = (-1,-1)
d = sqrt( (x1-x2)^2 + (y1-y2)^2 )
d = sqrt( (-3-(-1))^2 + (3-(-1))^2 )
d = sqrt( (-3+1)^2 + (3+1)^2 )
d = sqrt( (-2)^2 + (4)^2 )
d = sqrt( 4 + 16 )
d = sqrt( 20 )
Segment AB is exactly sqrt(20) units long.
This is side c since angle C is opposite this side.
Repeat similar steps for BC and AC.
The sides of triangle ABC are
a = segment BC = sqrt(20)
b = segment AC = sqrt(72)
c = segment AB = sqrt(20)
Now we can use the law of cosines to find angle A
a^2 = b^2 + c^2 - 2*b*c*cos(A)
(sqrt(20))^2 = (sqrt(72))^2 + (sqrt(20))^2 - 2*sqrt(72)*sqrt(20)*cos(A)
20 = 72+20 - 2*sqrt(72)*sqrt(20)*cos(A)
20 = 92 - 2*sqrt(72*20)*cos(A)
20 - 92 = -2*sqrt(1440)*cos(A)
-72 = -2*sqrt(144*10)*cos(A)
-72 = -2*sqrt(144)*sqrt(10)*cos(A)
-72 = -2*12*sqrt(10)*cos(A)
-72 = -24*sqrt(10)*cos(A)
cos(A) = -72/(-24*sqrt(10))
cos(A) = 0.94868329805051
A = arccos(0.94868329805051)
A = 18.4349488229227
A = 18.435
Angle A is roughly 18.435 degrees.
Since triangle ABC is isosceles, this means angle C is also this approximate measure.
The congruent angles are opposite the congruent sides. Use the law of cosines to confirm this statement.
The remaining angle B is,
A+B+C = 180
B = 180-(A+C)
B = 180-(18.4349488229227+18.4349488229227)
B = 143.130102354154
B = 143.130
Summary:
Angle A = 18.435 degrees
Angle B = 143.130 degrees
Angle C = 18.435 degrees
Each value is approximate.
Round these values according to the instructions your teacher gives you.
|
|
|
| |