|
Question 1195474: Determine if the points (3,5), (3,3) and (2,4) are the vertices of a right triangle. Explain your rationale.
Found 2 solutions by Alan3354, ikleyn:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! Determine if the points A(3,5), B(3,3) and C(2,4) are the vertices of a right triangle. Explain your rationale.
--------------
Slope of AC = diffy/diffx = (3-2)/(5-4) = 1
Slope of BC = ((3-2)/(3-4) = -1
---> perpendicular --> a right triangle
Answer by ikleyn(52865)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Determine if the points (3,5), (3,3) and (2,4) are the vertices of a right triangle.
Explain your rationale.
~~~~~~~~~~~~
Points A = (3,5) and B = (3,3) have the same x-coordinate.
It means that both points A and B lie on vertical line x= 3, parallel to y-axis.
Next, points A = (3,5) and C = (2,4) have different y-coordinates; hence, line AC is not horizontal.
Similarly, points B = (3,3) and C = (2,4) have different y-coordinates; hence, line BC is not horizontal.
Thus, line AB is vertical, but angles A and B are not right angles.
So, we only should check if lines AC and BC are perpendicular.
Line AC has the slope 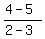 = = 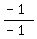 = 1.
Line BC has the slope = 1.
Line BC has the slope 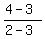 = =  = -1.
Thus lines AC and BC are perpendicular, since their slopes are 1 and -1, i.e. negatively reciprocal
(their product is 1 * (-1) = -1).
ANSWER. Angle C is the right angle. = -1.
Thus lines AC and BC are perpendicular, since their slopes are 1 and -1, i.e. negatively reciprocal
(their product is 1 * (-1) = -1).
ANSWER. Angle C is the right angle.
Solved.
|
|
|
| |