.
Find the area of the largest equilateral triangle that can be inscribed
in a circle whose diameter is 20cm.
~~~~~~~~~~~~~~~~~~
How the problem is worded, it shows that its composer has
.
The correct formulation SHOULD NOT speak about the largest equilateral triangle
that can be inscribed in a circle of a given radius, because all such triangles are congruent
and have the same area - - - there is NO the " largest " such a triangle.
So, I will solve the problem in that UNIQUE (modified) formulation which is correct :
Find the area of an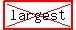 
equilateral triangle
inscribed in a circle whose diameter is 20 cm.
Solution
The sine law theorem says that if any triangle is inscribed in a circle of a radius R, then
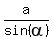= 2R,
where "a" is any of the three sides of the triangle and 
is an opposite angle.
In our case, all the angles of the equilateral triangle have the same measure of 60°, so
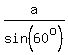= 2*10,
(R = 10 cm is the radius of the circle), which implies
a =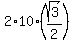 
= 
centimeters.
Next, the area of an equilateral triangle with the side "a" is 
.
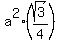Therefore, the area of our triangle is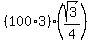 
= 
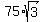cm^2 = 129.9038 cm^2, approximately. ANSWER
Solved.
-----------------
To see the Sine law theorem in this formulation, look into the lesson
- Law of sines - the Geometric Proof
Happy learning (!)
