Question 1191271: Find the equation of the circle having the points (2,10) and (-8,-14) the ends of its diameter.
Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!
Any circle has two defining properties:
Let's first find the center.
This is the same as finding the midpoint of those two endpoints on the diameter.
Focus on the x coordinates for now.
Add them up: 2+(-8) = -6
Divide the result in half: -6/2 = -3
This is the x coordinate of the midpoint.
Repeat those steps for the y coordinates:
Add: 10+(-14) = -4
Divide by two: -4/2 = -2
This is the y coordinate of the midpoint.
The midpoint is located at (-3,-2)
This is the center of the circle.
Center = (h,k) = (-3,-2)
Or to break it down further, we have h = -3 and k = -2 pair up together.
Now to find the radius.
The radius is the distance from the center to any point on the edge of the circle.
I'll use the distance formula to calculate the distance from the endpoint (2,10) to the center (-3,-2)
(x1,y1) = (2,10) and (x2, y2) = (-3,-2)
^2 + (y_1 - y_2)^2})
)^2 + (10-(-2))^2})
^2 + (10+2)^2})
^2 + (12)^2})
The distance from (2,10) to (-3,-2) is exactly 13 units.
Therefore, the radius is r = 13.
-------------------
To recap, we found:
h = -3
k = -2
r = 13
The circle template  will update to  after plugging in those values mentioned.
Simplifying things gets us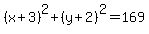 
Graph:
The diagram was made using GeoGebra.
Answer: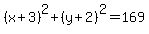
Center = (-3,-2) and radius = 13
|
|
|
