Question 1187084: What is the equation of the circle with center at(0.2) and tangent to the line
3x-4y=12
Found 2 solutions by Alan3354, ikleyn:
Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website! What is the equation of the circle with center at(0.2) and tangent to the line
3x-4y=12
----------------
There's a formula for the distance from a point to a line, but I'll work it the "long way."
---------
3x-4y=12 ---> y = (3/4)x - 3
Slope of the line is 3/4
Slope of lines perpendicular is -4/3
(0,2) is the y intercept ---> y = (-4/3)x + 2
Find the intersection of the 2 lines.
---
y = (3/4)x - 3
y = (-4/3)x + 2
---
(3/4)x - 3 = (-4/3)x + 2
9x - 36 = -16x + 24
25x = 60
x = 2.4
y = -1.2
Intersection at (2.4,-1.2)
Distance from (0,2) = sqrt(diffy^2 + diffx^2) = sqrt(2.4^2 + 3.2^2) = sqrt(16) = 4
-------
 is the circle
Answer by ikleyn(52835)  (Show Source):
You can put this solution on YOUR website! .
What is the equation of the circle with center at 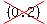 (0,2) and tangent to the line 3x-4y=12.
~~~~~~~~~~~~~~~~~~
All you need to do is to find the distance from the point (0,2) to the given straight line 3x - 4y - 12 = 0.
There is a remarkable formula which ideally suits for this need.
Let the straight line in a coordinate plane is defined in terms of its linear equation
a*x + b*y + c = 0,
where "a", "b" and "c" are real numbers, and let P = ( , ) be the point in the coordinate plane.
Then the distance from the point P to the straight line is equal to
d =  .
Regarding this formula, see the lesson
The distance from a point to a straight line in a coordinate plane
in this site.
Substitute the given data a= 3, b= -4, c= -12, = 0, = 2 into the formula to get the distance under the question
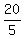 =  = 4.
Thus the radius of the circle is 4 units.
THEREFORE, the circle equation is
 +  =  ,
or
 + = 16. ANSWER
Solved.
|
|
|
