SOLUTION: Given two lines 2x - y - 1 = 0 …eq. 1and 3x + y - 4= 0 …eq. 2, and point A (0, 4) lying on eq. 2, find the equation of the line which is symmetric to eq. 2 with respect to eq.

Get some graph paper and plot the lines:



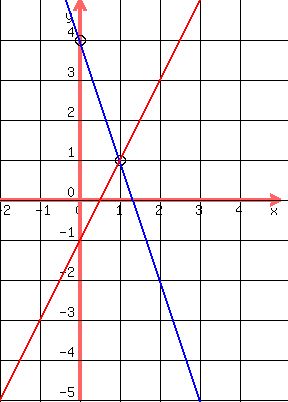The red line is the line 2x-y-1=0, eq.1
The blue line is the line 3x+y-4=0, eq.2

They cross at the point (1,1)

Notice that to get from the point where they cross (1,1)
we have to go left 1 unit and then up 3 units.  That's
indicated by the green lines:



Now this time starting at (1,1) and go right as many units
as you went up before, and up as many units as you went
left before, like the other green lines below:



You see that you ended up at the point (4,2).

Now draw a line through (1,1) and (4,2), like this black
line below:



That black line is the line which is symmetric to eq. 2 with
respect to eq. 1. 

We find its equation.  It goes through (1,1) and (4,2).

We use the slope formula:

.

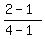Then we use the point-slope form:





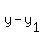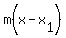
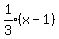Multiply through by 3





or, multiplying by -1

  <-- the equation of the black line.

Edwin