Question 1180635: Two pulleys are connected by a belt. The radii of the pulleys are 6 cm and 21 cm, and the distance between
their centers is 30 cm. Find the total length of belt needed to connect the pulleys.
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Two pulleys are connected by a belt. The radii of the pulleys are 6 cm and 21 cm, and the distance between
their centers is 30 cm. Find the total length of belt needed to connect the pulleys.
~~~~~~~~~~~~~~~~~~~~~
@MathLover used the formula from this web-site
https://www.sudenga.com/practical-applications/figuring-belt-lengths-and-distance-between-pulleys
without referencing.
At that web-site, the formula is given without derivation or explanations.
Therefore, I developed here the full solution with detailed derivation of all formulas -
- partly to check her calculations and partly to have a full derivation.
Our results are close enough.
The key here is to note that the point at which the belt just leaves or enters the pulleys, is a point of tangency,
that is, the segment connecting these points on the two pulleys are at right angles to the radii of both pulleys.
Let this segment length be x cm for my following calculations. Draw a line starting from the center of the 6 cm pulley parallel
to the tangent line until it intersects with the 21 cm radius of the larger pulley.
You now have a right triangle with legs x and 15 cm = 21 cm - 6 cm, with hypotenuse the given distance between the centers
of the pulleys = 30 cm.
You now can calculate with the Pythagorean theorem x = 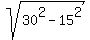 = = 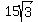 = 25.98 cm.
All you need to do next is calculate the rest of the belt that remains on the pulleys.
By using the (x,15,30) right triangle, you can determine the central angles of the arcs of each pulley that the belts are on.
Note for the small pulley the central angle is less than 180°, and greater than 180° for the larger pulley.
The acute angle of this triangle at the center of larger pulley is
a = = 25.98 cm.
All you need to do next is calculate the rest of the belt that remains on the pulleys.
By using the (x,15,30) right triangle, you can determine the central angles of the arcs of each pulley that the belts are on.
Note for the small pulley the central angle is less than 180°, and greater than 180° for the larger pulley.
The acute angle of this triangle at the center of larger pulley is
a = 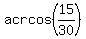 = = 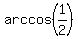 = =  = = 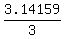 = 1.0472 radians, or 60°.
That part of the belt remaining on the pulleys can now be calculated by multiplying the central angle by
the radius of the respective pulleys.
For the greater pulley, the central angle is = 1.0472 radians, or 60°.
That part of the belt remaining on the pulleys can now be calculated by multiplying the central angle by
the radius of the respective pulleys.
For the greater pulley, the central angle is 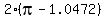 radians;
THEREFORE, the belt remaining on the greater pulley is of G = 2*(3.14159-1.0472)*21 = 87.9644 cm long.
For the greater pulley, the central angle is radians;
THEREFORE, the belt remaining on the greater pulley is of G = 2*(3.14159-1.0472)*21 = 87.9644 cm long.
For the greater pulley, the central angle is 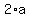 radians;
THEREFORE, the belt remaining on the greater pulley is of S = 2*1.0472*6 = 12.56 cm long.
Now the total length of belt is the sum 2x + G + S = 2*25.98 + 87.96 + 12.56 = 157.04 cm. radians;
THEREFORE, the belt remaining on the greater pulley is of S = 2*1.0472*6 = 12.56 cm long.
Now the total length of belt is the sum 2x + G + S = 2*25.98 + 87.96 + 12.56 = 157.04 cm.
Solved.
|
|
|