|
Question 117796: Is triangle MNP with vertices M(1,4), N(-3,-2), and P(4,-3) and isosceles triangle? Explain.
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! This triangle is formed by the three lines ... line MN, line NP, and line PM
.
The way you solve this is to use the distance formula to find the lengths of these each of the
three lines. If two of the lines have the same distance, then the triangle is isosceles.
.
The distance formula says that the distance (D) between two points is given by the equation:
.

.
To use this formula, all you have to do is call one of the end points of a line point 2, the
point at the other end of the line point 1, and substitute the resulting values appropriately
into the formula.
.
Let's begin with Line MN. Give point N the label "point 2" so that its x and y values have the
subscript 2. So we can say  and and  . Give point M (the point at the . Give point M (the point at the
other end of Line MN) the label "point 1" so the x and y values of point M have the subscript
1 and we can say that for this line  and and  . Now that we have . Now that we have
identified the four values for Line MN we can substitute those values into the distance equation.
Start with the distance equation:
.

.
Make the four substitutions of x and y values:
.

.
Combine the numbers in the parentheses to get:
.

.
Square each of the two terms:
.

.
Combine the numbers under the radical sign:
.

.
So the length of Line MN is  . .
.
Next, let's do the same thing for Line NP which has as its endpoints the two points N (-3, -2)
and P (4, -3). Give point P the label "point 2" so that its x and y values have the
subscript 2. So we can say  and and  . Give point N (the point at the . Give point N (the point at the
other end of Line NP) the label "point 1" so the x and y values of point N have the subscript
1 and we can say that for this line  and and  . Now that we have . Now that we have
identified the four values for Line NP we can substitute those values into the distance equation.
Start with the distance equation:
.

.
Make the four substitutions of x and y values:
.

.
Combine the numbers in the parentheses to get:
.

.
Square each of the two terms:
.

.
Combine the numbers under the radical sign:
.

.
So the length of Line NP is 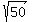 . .
.
Finally, let's do the same thing for Line MP which has as its endpoints the two points M (1, 4)
and P (4, -3). Give point P the label "point 2" so that its x and y values have the
subscript 2. So we can say  and and  . Give point M (the point at the . Give point M (the point at the
other end of Line MP) the label "point 1" so the x and y values of point M have the subscript
1 and we can say that for this line  and and  . Now that we have . Now that we have
identified the four values for Line MP we can substitute those values into the distance equation.
Start with the distance equation:
.

.
Make the four substitutions of x and y values:
.

.
Combine the numbers in the parentheses to get:
.

.
Square each of the two terms:
.

.
Combine the numbers under the radical sign:
.

.
So the length of Line MP is 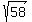 . .
.
Notice that the lengths of the three sides of triangle MNP are:
.

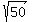 and and
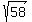
.
All the sides of this triangle have different lengths and therefore the triangle cannot be
isosceles because an isosceles triangle must have two sides of the same length.
.
Hope this helps you to understand the problem and how to solve it.
.
.
|
|
|
| |