Question 1165093: A seismological station is located at (0 ,3), 3 km away from a straight shoreline
where the x-axis runs through. The epicenter of an earthquake was determined to
be 6 km away from the station.
(a) Find the equation of the curve that contains the possible location of the
epicenter.
(b) If furthermore, the epicenter was determined to be 2 km away from the shore,
find its possible coordinates (rounded off to two decimal places).
Answer by MathLover1(20854)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Here we have a circle, so the equation will be in  where ( where ( , ,  ) is the center of the circle. ) is the center of the circle.
For part a, the radius  of the circle representing the possible locations of the epicenter is the distance from the station to the epicenter, which is of the circle representing the possible locations of the epicenter is the distance from the station to the epicenter, which is km. km.
Since given that the station is at ( , , ), the center of the circle is at that point, and the equation becomes ), the center of the circle is at that point, and the equation becomes


This is the equation of the curve that contains the possible location of the epicenter.
For part b, when the epicenter is 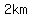 away from the shore, we need to find the away from the shore, we need to find the  -coordinates where -coordinates where  . .
Substitute  into the equation into the equation  : :





solutions:  or or 
so, the coordinates of the epicenter are (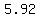 , ,  ) or ( ) or (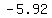 , ,  ) )
|
|
|