|
Question 1163111: N lattice points in coordinate 8-space are chosen at random. The line segments joining all pairs of these N points are drawn. What is the smallest value of N that guarantees that the midpoint of at least one of the resulting line segments is itself a lattice point?
(A) 256 (B) 255 (C) 17 (D) 257 (E) 16
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! N lattice points in coordinate 8-space are chosen at random. The line segments joining all pairs of these N points are drawn.
What is the smallest value of N that guarantees that the midpoint of at least one of the resulting line segments is itself a lattice point?
~~~~~~~~~~~~~~~
Each lattice point x = ( , ,  , ,  , . . . , , . . . , 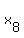 ) is the set of 8 (eight) integer numbers, - its coordinates,
that are positive, zero or negative integer numbers.
The line segments, joining all pairs of these lattice points, are vectors, whose components are the differences of the
lattice points' coordinates.
For each such a joining segment/vector, its midpoint is a lattice point if and only if ALL 8 components of this segment/vector
are EVEN numbers.
As I just said above, each component of the joint segment/vector is the difference of the coordinates of the original
lattice points.
Therefore, for every joining segment/vector, its midpoint is a lattice point if and only if for the respective pair of the lattice points
all 8 their coordinates have the same parity as integer numbers, i.e. in each of 8 positions they are either EVEN or ODD integer
numbers simultaneously.
Next, it is clear, that in any set of ) is the set of 8 (eight) integer numbers, - its coordinates,
that are positive, zero or negative integer numbers.
The line segments, joining all pairs of these lattice points, are vectors, whose components are the differences of the
lattice points' coordinates.
For each such a joining segment/vector, its midpoint is a lattice point if and only if ALL 8 components of this segment/vector
are EVEN numbers.
As I just said above, each component of the joint segment/vector is the difference of the coordinates of the original
lattice points.
Therefore, for every joining segment/vector, its midpoint is a lattice point if and only if for the respective pair of the lattice points
all 8 their coordinates have the same parity as integer numbers, i.e. in each of 8 positions they are either EVEN or ODD integer
numbers simultaneously.
Next, it is clear, that in any set of 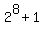 vectors with integer components in 8-space vectors with integer components in 8-space 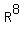 , at least two vectors have identical parity
of integer components in all 8 positions.
+-------------------------------------------------+
| It follows from the "pigeonhole principle". |
+-------------------------------------------------+
It leads us to the conclusion that if , at least two vectors have identical parity
of integer components in all 8 positions.
+-------------------------------------------------+
| It follows from the "pigeonhole principle". |
+-------------------------------------------------+
It leads us to the conclusion that if  (the number of all joining segments) is greater than (the number of all joining segments) is greater than 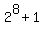 = 257,
then there are at least two vectors that have identical parity of integer components in all 8 positions.
Therefore, the minimal number N the problem asks for, is N satisfying inequality = 257,
then there are at least two vectors that have identical parity of integer components in all 8 positions.
Therefore, the minimal number N the problem asks for, is N satisfying inequality
 >= 257, or
N*(N-1) >= 2*257 = 514.
And since >= 257, or
N*(N-1) >= 2*257 = 514.
And since 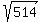 = 22.67, the final inequality and the ANSWER is N >= 24.
ANSWER. The smallest value of N that guarantees that the midpoint of at least one of the resulting line segments is itself a lattice point, is 24. = 22.67, the final inequality and the ANSWER is N >= 24.
ANSWER. The smallest value of N that guarantees that the midpoint of at least one of the resulting line segments is itself a lattice point, is 24.
Solved.
/\/\/\/\/\/\/\/
The post-solution notice:
This value of 24 is not in your post answers list, meaning that the post is/was DEFECTIVE.
Thanks for submitting this remarkable problem.
|
|
|
| |