Question 1152378: Question 8
If AB = 5.5, CD = 7, and FE = 19.5, calculate the values of line segment AE and line segment CE
image of a circle inscribed inside triangle ACE; the points of intersection points are: on side AC point B, on side AE point F, and on side CE point D
AE = 25 and CE = 26
AE = 26.5 and CE = 25
AE = 25.5 and CE = 26.5
AE = 25 and CE = 26.5
2 points
Question 9
If BD = 2.4 and AB = 1.0, calculate the value of DA.
circle D with tangent line segment AC touching at point B; line segment AD
1.96
2.18
11.56
2.6
2 points
Question 10
If AB = 9, CD = 12, and FE = 22, calculate the values of line segment AE and line segment CE
image of a circle inscribed inside triangle ACE; the points of intersection points are: on side AC point B, on side AE point F, and on side CE point D
AE = 34 and CE = 31
AE = 31 and CE = 34
AE = 21 and CE = 34
AE = 34 and CE =21
2 points
Question 11
What is true about the construction of a regular hexagon inscribed in a circle?
The circle is tangent to each side of the hexagon.
All of the vertices of the hexagon lie outside the circle.
All of the vertices of the hexagon lie inside the circle.
The circle intersects each vertex of the hexagon.
2 points
Question 12
Which of the following shows a circle passing through three non-collinear points, A, B, and C?
an inscribed circle has each of its vertices on the circle
circle circumscribed about triangle
circle with two chords, and two secants each passing through the center; chords divided into congruent segments by secants
circle with two chords marked AB and BC, chord AB is bisected by segment OC and chord BC is bisected by an unlabeled segment passing through the center of the circle
2 points
Question 13
Which of the following is true about the following construction of a tangent to a circle from a point outside of the circle?
circle O with point B outside circle O, dashed segment connecting points O and B, point M located on segment O B, point M is the midpoint of O B, points X and Y located on circle O such that segments B X and B Y are tangent to circle O at points X and Y respectively, tangents B X and B Y drawn in blue, dashed arc shown going through points X O and Y.
A.m
B.OM=MB
C.OX=OM
D.m
d.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
given:  , ,  , and , and 
If two segments from the same exterior points are tangent to a circle, then they are congruent. Since 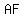 and and  are segments from the same exterior point ( are segments from the same exterior point ( ), then ), then
 and and 
Since  and and  are segments from the same exterior point ( are segments from the same exterior point ( ), then ), then
 and and 
Since  and and 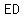 are segments from the same exterior point ( are segments from the same exterior point ( ), then ), then
 and and 






Therefore,
 and and 
Question 9
If  and and  , calculate the value of , calculate the value of 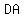 . .
circle  with tangent line segment with tangent line segment  touching at point touching at point ; line segment ; line segment 
If a line is tangent to a circle, then it is perpendicular to the radius, making  a right triangle. a right triangle.
Since you have to calculate 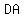 , use the Pythagorean Theorem. , use the Pythagorean Theorem.






Question 10
If  , ,  , and , and  , calculate the values of line segment , calculate the values of line segment 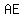 and line segment and line segment 
image of a circle inscribed inside triangle 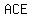 ; the points of intersection points are: on side ; the points of intersection points are: on side  point point  , on side , on side 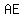 point point  , and on side , and on side  point point 
Tangents to a circle from the same point are the same length, so


and,


The side lengths are
 , , 
Question 11
What is true about the construction of a regular hexagon inscribed in a circle?
answer:
The circle intersects each vertex of the hexagon.
Question 12.
Which of the following shows a circle passing through three non-collinear points, A, B, and C?
One and only one circle can be drawn through A, B, and C
answer: circle circumscribed about triangle
Question 13
Which of the following is true about the following construction of a tangent to a circle from a point outside of the circle?
Since the construction of the tangent of a circle from a point outside the circle is given by the following steps:
Draw a line connecting the point to the center of the circle.
Construct the perpendicular bisector of that line.
Place the compass on the midpoint, adjust its length to reach the end point, and draw an arc across the circle .
Where the arc crosses the circle will be the tangent points.
Hence from the first step we get a line segment 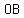 . .
now from the second step we get a perpendicular bisector of line 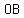 at point at point  . .
This means that  ( since bisector means that the line is cut into two equal parts) ( since bisector means that the line is cut into two equal parts)
Hence, option:  is correct. is correct.
answer: 
|
|
|