SOLUTION: The interior angles of a convex nonagon have degree measures that are integers in arithmetic sequence. What is the smallest angle possible in this nonagon?

From one side, the sum of interior angles of any 9-gon is  (9-2)*180 = 7*180 degrees.


From the other side, the sum of the first n terms of any arithmetic progression is


     = .


In our case, 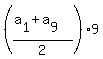  = 7*180,  so


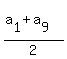     = 140  degrees.


For arithmetic progression, the average of any two terms, equally remoted from the central term, is the same.


In particular, the central term   is 140 degrees.


The terms of the AP are


     = 140 -  d,    = 140 +  d,

     = 140 - 2d,    = 140 + 2d,

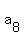     = 140 - 3d,    = 140 + 3d,

     = 140 - 4d,    = 140 + 4d.


To make  as small as possible, we should take the common difference as large as possible.


We have two constraints:   must be positive,   > 0,                                      (1)

and
                           must be less than 180 degrees;  so    must be 176 degrees.    (2)


Of these two constraints, the constraint (2) is more cumbersome, and it gives

    d = 36/4 = 9 degrees.


Then both constraints (1) and (2) are satisfied.


Thus the minimum angle is   = 140 - 4*9 = 140 - 36 = 104 degrees.    ANSWER