Question 1150673: Which one of these circles has the smallest area?
- x² + y² = 12
- (x - 2)² + y² = 8
- (x + 1)² + (y+3)² = 6
- (x + 8)² + (y - 9)² = 3
(The only way to find out is to find the area of each of these answer choices, and then select the SMALLEST area, by using these formulas:)
(x + h)² + (y + k)² = r²
Center = (h, k)
Radius = √(r²) or r
Found 3 solutions by Alan3354, Kimani, ikleyn:
Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website! Which one of these circles has the smallest area?
- x² + y² = 12
- (x - 2)² + y² = 8
- (x + 1)² + (y+3)² = 6
- (x + 8)² + (y - 9)² = 3
(The only way to find out is to find the area of each of these answer choices, and then select the SMALLEST area, by using these formulas:)
---------------
No. Find the one with the smallest radius.
---> smallest area
==========================
Answer by Kimani(1)  (Show Source):
You can put this solution on YOUR website! So, basically, when I placed these values on my TI-84 Plus graphing-calculator from Texas Instruments...
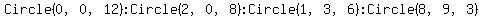
...and then pressed the [ENTER] key, the graph automatically draws 4 different circles that are roughly interlinking each other—but in different sizes—and as I watched each step carefully, I have recognized that the smallest circle is the one with the radius of 3.
Although the center is located at coordinates (8, 9), the radius of the circle is measured 3 units for all 360 angles, no matter what the selected angle.
So, therefore, (x + 8)² + (y - 9)² = 3 is the circle that has the smallest area, or radius.
Answer by ikleyn(52851)  (Show Source):
You can put this solution on YOUR website! .
The hint in your post is absolutely ineffective.
The most reasonable and effective way is to quickly select the case, where the radius of the circle
(or, equivalently, the square of the radius, which is the right side of the equation) is smallest.
You do not need to use a computer or a calculator for it, as the other person suggests.
It is enough to look on equations and turn on your brain (which is inside your head).
|
|
|
