SOLUTION: I would appreciate if someone could help me on this problem-please if you could show the work so I can understand it. Thanks A pirate sails in a circular route around point A,

Algebra ->  Circles -> SOLUTION: I would appreciate if someone could help me on this problem-please if you could show the work so I can understand it. Thanks A pirate sails in a circular route around point A,       Log On


   

Question 1145856: I would appreciate if someone could help me on this problem-please if you could show the work so I can understand it. Thanks
A pirate sails in a circular route around point A,
as shown to the right, with a circumference of
32 km, and a merchant ship sails in a circular
route around point B with a circumference of 48 km.
If they both start where the routes meet, and the pirate
sails 12 km per day and the merchant sails at 8 km per
day, what is the least number of days later they will
next meet?
CHOICE ANSWERS GIVEN BELOW:
A) 8 days B) 16 days C) 24 days D) 32 days
Found 3 solutions by Alan3354, greenestamps, ikleyn:
Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
Nothing is shown to the right.

Answer by greenestamps(13203) About Me  (Show Source):
You can put this solution on YOUR website!


The pirate ship makes one complete circle every 32/12 = 8/3 days.

The merchant ship makes one complete circle every 48/8 = 6 days.

The number of days until they are again at the same point is the least common multiple of 8/3 and 6.

It's a bit unusual to need to find the LCM of two numbers where one of them is a fraction. So let me show the way I prefer for finding the least common multiple of ANY two numbers.

(1) Make a fraction with the two numbers as the numerator and denominator:

%288%2F3%29%2F6

(2) Simplify the fraction to where the numerator and denominator are whole numbers with no common factor:

%288%2F3%29%2F6+=+8%2F18+=+4%2F9

(3) Write the equation that says the original fraction and the simplified fractions are equivalent:

%288%2F3%29%2F6+=+4%2F9

(4) Cross multiplying in either direction will give you the LCM:

%288%2F3%29%2A9+=+8%2A3+=+24
6%2A4+=+24

So the least common multiple of 8/3 and 6 is 24.

ANSWER C: 24 days

Answer by ikleyn(52855) About Me  (Show Source):
You can put this solution on YOUR website!
.

            First of all, nothing is shown to the right, although the post promises it.

            I understand your difficulties. In such case, you MUST provide an adequate wording description.

            I strongly (strictly) suspect that these circles touch each other, having one (and only one) common point. 

            (Simply because I do not see any other alternative possibility).

            If so (I am 129% confident it is so), then the solution can be easily done as follows. 


The pirate' ship makes 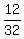 12%2F32 = 3%2F8 of his circle per day.

It needs 8 days to make 3 circles, and it makes integer number of circles every 8 days  (as a check, 8*12 = 96 = 32*3 miles.)



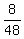The merchant ship makes  8%2F48 = 1%2F6 of his circle per day.

It needs 6 days to make 1 circle, and it makes integer number of circles every 6 days  (as a check, 6*8 = 48 = 48 miles.)



The two ships can meet each other at the touching point ONLY, and

for it, each ship should make integer number of their corresponding circles.



Therefore, we should find the Least Common Multiple of the integer numbers 8 and 6.


This LCM = LCM(8,6) = 24.



ANSWER.  In 24 days.


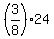CHECK.  In 24 days, the pitate' ship will make %283%2F8%29%2A24 = 9 full circles;

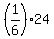        in 24 days, the merchant ship will make  %281%2F6%29%2A24 = 4 full circles.

        Thus after 24 days each of them will complete the integer number of their corresponding circles 
        and, hence, they will meet each other again for the first time.

Solved.