SOLUTION: Find the distance between the pair of parallel lines. y = 2x + 4 y = 2x - 4

Actually, the distance between two parallel lines on a plane is the length of (any) perpendicular between these lines.


To find the distance in this case, take any point on one line and calculate its distance from the second line.


For simplicity, put x= 0 and from the first equation find  y= 2*0 + 4 = 4.

Thus the point (0,4) lies on the first line.


To find the distance from this point (0,4) to the line y = 2x - 4, use the general formula

for the distance from the point (p,q) on the coordinate plane to the line  Ax + BY + C = 0


    d = .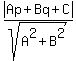


In your case the point is (0,4) and the line is 2x - y - 4 = 0,  so  A= 2, B= -1, C= -4, p= 0  and  q= 4,

and the formula (1) takes the form


    d = 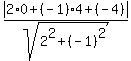 =  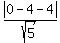=  =  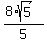= 3.577 (approximately).   ANSWER