Question 1144303: Find the equation of the circle if it is touching the line x+y=8 at (2,6) and passing through (4,0)
Answer by greenestamps(13214)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The circle touches the line x+y=8 at (2,6); i.e., it is tangent to that line at that point. That means the center of the circle is on the line that is perpendicular to the given line at that point.
The given line has a slope of -1, so the line containing that radius has a slope of 1. Since it passes through (2,6), the equation of the line containing that radius is y=x+4.
So let an arbitrary point on the line containing the center of the circle be (a,a+4). We need the distances from (a,a+4) to (2,6) and from (a,a+4) to (4,0) to be the same.
It is easier to solve the problem using the squares of the distances....
square of the distance from (a,a+4) to (2,6): 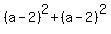
square of the distance from (a,a+4) to (4,0): 
Then





The center of the circle is (a,a+4) = (-3,1).
CHECK:
distance from (-3,1) to (2,6) = 
distance from (-3,1) to (4,0) = 
|
|
|