Question 1142649: Find the equation of the circle tangent to  at (-3,0) and at (-3,0) and
contains the point (-3,-6). Thank you!
Answer by ikleyn(52897)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The center of this circle lies on the straight line perpendicular to the given line and passing through the point (-3,0).
From the other side, the center of this circle lies on the perpendicular bisector to the segment connecting the points (-3,0) and (-3,6).
Notice that this segment, connecting the points (-3,0) and (-3,6), is VERTICAL and its middle point is (-3,3).
So, that perpendicular bisector is simply the horizontal line y = 3.
Perpendicular to the given line has an equation
3x + 2y = c, (1)
where "c" is unknown constant.
Since this perpendicular line (1) passes through the point (-3,0), we have
3*(-3) + 2*0 = c = -9.
Thus, the center of the circle lies on the line
3x + 2y = -9
and on the line y =3 at the same time, which gives you
3x + 2*3 = -9,
3x = -9 - 6 = -15,
x = -15/3 = -5.
Thus the center of the circle is the point (x,y) = (-5,3).
Since the distance from the center of the circle to the point (-3,0) is
 = = 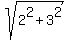 = =  ,
the radius of the circle is ,
the radius of the circle is  .
Then the equation of the circle in the standard form is .
Then the equation of the circle in the standard form is
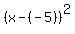 + + 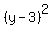 = =  ,
or, equivalently, ,
or, equivalently,
 + + 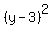 = 13. ANSWER = 13. ANSWER
----------------
If you want to see many other similar solved problems, you can find them in the lesson
- Find the standard equation of a circle
in this site.
|
|
|