Question 1140775: (1) A cirlce is defined by the equation x^2-6x+y^2-2y=6.
(a) Rewrite the equation of the circle in the form:(x-a)^2+(y-b)^2=r^2
(b) Write down the coordinates of M,the centre of the circle.
(c) A tangent PQ is drawn from the point P(6;-2) to the circle, with Q the point of contact.Calculate the length of the tangent PQ.
Please can someone please help me with the question I begg
Found 2 solutions by MathLover1, greenestamps:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! (1) A cirlce is defined by the equation  . .
(a) Rewrite the equation of the circle in the form:

 ............complete square ............complete square
 ....... ....... for for  part is part is  and and  for for  part is part is 






(b) Write down the coordinates of M,the centre of the circle.
since  and and  , ,
the coordinates of M are: ( , , )=( )=( , , ) )
(c) A tangent PQ is drawn from the point P( ; ; ) to the circle, with ) to the circle, with  the point of contact.Calculate the length of the tangent the point of contact.Calculate the length of the tangent  . .
if  is a tangent, it is perpendicular to the radius is a tangent, it is perpendicular to the radius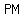
points  , , , and , and  form right triangle where form right triangle where 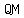 is hypotenuse, is hypotenuse, 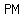 and and  are legs are legs
we can find the length of 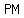 using points P( using points P( ; ; ) and M( ) and M( , , ) )





 ->one leg ->one leg
and
 , the other leg will be: , the other leg will be:
P( ; ; ) and Q( ) and Q( , , ) )

then we can find hypotenuse 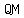 : :
 ( ( , , ) and ) and  ( ( , , ) )

using Pythagorean theorem:






 .............=>so point .............=>so point  ( ( , , ) )
then substitute in Pythagorean theorem:

 ........solve for ........solve for 



and, then
 => =>
so  ( ( , , ) )
the length of the tangent  is: distance between is: distance between
 ( ( ; ; ) )
 ( ( , , ) )




double check:




tangent is a line passing through points P( ; ; ) and ) and  ( ( , , ), so find equation ), so find equation
first find a slope:



and use slope point formula


 -> tangent line -> tangent line
line that passes through 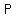 and and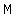 is perpendicular to tangent and it is: is perpendicular to tangent and it is:



and use slope point formula






Answer by greenestamps(13200)   (Show Source): (Show Source):
|
|
|