SOLUTION: 13. Find the center of the circle x^2+y^2-(2k+1)x+(1-k)y-3=0 lies on x-y+2=0 14. C_1 And C_2 are two concentric circles with C_1:x^2+y^2-2x-4y-4=0 If C_2 divided C_1 into two

Algebra ->  Circles -> SOLUTION: 13. Find the center of the circle x^2+y^2-(2k+1)x+(1-k)y-3=0 lies on x-y+2=0 14. C_1 And C_2 are two concentric circles with C_1:x^2+y^2-2x-4y-4=0 If C_2 divided C_1 into two       Log On


   

Question 1134829: 13. Find the center of the circle x^2+y^2-(2k+1)x+(1-k)y-3=0 lies on x-y+2=0
14. C_1 And C_2 are two concentric circles with C_1:x^2+y^2-2x-4y-4=0
If C_2 divided C_1 into two equal parts, find the equation of C_2
15. Given that x^2+y^2+2(m+1)x-2my+3m^2-2=0 represents a circle
Find the value of m so that it has the maximum area.
Answer by ikleyn(52803) About Me  (Show Source):
You can put this solution on YOUR website!
.

I will solve only the first problem from the post.

But before to start,  I'll re-formulate this #1 problem in a way to make sense. 

 
    Find the value k in a way the center of the circle x^2+y^2-(2k+1)x+(1-k)y-3=0 lies on x-y+2=0.


Solution 

To find the center of the circle, you should complete the squares in the left side of the equation.


I will omit the steps assuming that you can do it on your own (or can do it MENTALLY), and only will give

the coordinates of the center that result from completing the squares.


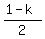The center of the circle is at  (-%282k%2B1%29%2F2,%281-k%29%2F2).


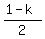Thus the coordinates of the center are  x%5B0%5D = -%282k%2B1%29%2F2,  y%5B0%5D = %281-k%29%2F2.    (1)


Now, we are given that the center  (x%5B0%5D,y%5B0%5D)  lies on the straight line  x - y + 2 = 0.


It means that  x%5B0%5D - y%5B0%5D + 2 = 0,   or


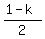    -%282k%2B1%29%2F2 - %281-k%29%2F2 + 2 = 0.


It is your equation to find the value of k.  Now simplify it step by step


    -(2k+1) = 1-k - 4,

    -2k - 1 = 1 - k - 4

     4 - 1 - 1 = -k + 2k

     k = 2.


Thus the problem is just solved, and the ANSWER  is  k = 2.


CHECK.  At k= 2, the center is, according (1),  the point  (x%5B0%5D,y%5B0%5D) = (-5%2F2,-1%2F2),  and  

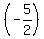        x%5B0%5D - y%5B0%5D + 2 = %28-5%2F2%29 - %28-1%2F2%29 + 2 = %28-5%2B1%29%2F2 + 2 = -2 + 2 = 0.     ! Correct !

--------------------

Now, let me explain you, why I solved only one problem #1 from your list. 

1.  First, the rules of this site require each post contains one and only one question/problem.


2.  I firmly believe, that if the tutor put more than one problem solution to his response, the result is such a mess 

    that learning from it becomes unsolvable task.


3.  And since I think that the major goal of this site/forum (and my personally) is to teach,

    I believe that this rule is absolutely fair and perfectly correct.  So I appeal to you to follow this rule.