SOLUTION: which has its center at the point (4:3)and touches the starting line 5x - 12y -10=0

Algebra ->  Points-lines-and-rays -> SOLUTION: which has its center at the point (4:3)and touches the starting line 5x - 12y -10=0      Log On


   

Question 1132079: which has its center at the point (4:3)and touches the starting line 5x - 12y -10=0
Answer by ikleyn(52878) About Me  (Show Source):
You can put this solution on YOUR website!
.

            The posted group of words has no any sense and needs to be edited to get a sense.

                                I edited it in this way: 


    Find the radius of the circle, which has the center at the point (4,3) and

    touches the straight line  5x - 12 - 10 = 0.



Solution 

All you need to do is to find the distance from the point (4,3) to the given straight line  5x - 12y - 10 = 0.


There is a remarkable formula which ideally suits for this need.


    Let the straight line in a coordinate plane is defined in terms of its linear equation 

         a*x + b*y + c = 0,

    where "a", "b" and "c" are real numbers, and let P = (x%5B0%5D,y%5B0%5D) be the point in the coordinate plane. 

    Then the distance from the point P to the straight line is equal to

        d = abs%28a%2Ax%5B0%5D+%2B+b%2Ay%5B0%5D+%2B+c%29%2Fsqrt%28a%5E2+%2B+b%5E2%29.


Regarding this formula, see the lesson
    The distance from a point to a straight line in a coordinate plane
in this site.


Substitute the given data  a= 5, b= -12, c= -10,  x%5B0%5D = 4,  y%5B0%5D= 3  into the formula to get the distance under the question

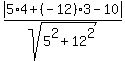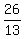    abs%285%2A4+%2B+%28-12%29%2A3+-+10%29%2Fsqrt%285%5E2%2B12%5E2%29 = 26%2F13 = 2.


Answer.  The radius of the circle is 2 units.

Solved.