Question 1130502: Find the equation of a circle whose center is on 2x+y=1, tangent to 3x-4y=10 and radius 5. thank you
Found 2 solutions by MathLover1, greenestamps:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
find intersection of line  and tangent and tangent 
 .......solve for .......solve for 

---------------------

substitute in 




then,


intersection point is:
P( 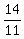 , ,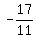 ) )
-> since center is on a line  , we have , we have

=>
so, center C ( , , )=( )=( , ,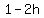 ) )
distance from  and and  is is



or


=>

or


so, we have two centers that lie on given line:
center C (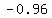 , ,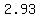 ) )
and
center C ( , , ) )
then, we have two circles:

or


Answer by greenestamps(13203)   (Show Source): (Show Source):
|
|
|