Question 1120006: A uniform wheel of 600mm diameter, weighing 5kN rests against a rigid rectangular block of 150mm height. Find the least pull, through the centre of the wheel, required just to turn the wheel over the corner A of a block. Also find the reaction of the block. Take all surfaces to be smooth
Found 2 solutions by solver91311, ikleyn:
Answer by solver91311(24713)   (Show Source): (Show Source):
Answer by ikleyn(52814)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A uniform wheel of 600mm diameter, weighing 5kN rests against a rigid rectangular block of 150mm height.
Find the least pull, through the centre of the wheel, required just to turn the wheel over the corner A of a block.
Also find the reaction of the block. Take all surfaces to be smooth
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Make a sketch. I will assume that you just did it and look in it.
The radius of the wheel is R = 300 mm 0.3 m.
The weight of 5 kN is applied at the center of the wheel and directed vertically down.
The force F (under the question) is applied horizontally at the center of the wheel.
As I said, it is directed horizontally, and it is directed to the block's side.
Draw the radius OA of the wheel from its center O to the point A where the wheel contacts with the block.
Notice that the angle the radius OA makes with the horizontal line is  = 30°.
It is because the radius of the wheel is 300 mm, while the height of the block is 150 mm.
The weight produces the moment of force = W*h, where the arm "h" is the horizontal projection of the radius OA
h = = 30°.
It is because the radius of the wheel is 300 mm, while the height of the block is 150 mm.
The weight produces the moment of force = W*h, where the arm "h" is the horizontal projection of the radius OA
h = 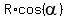 = R*cos(30°).
Therefore the moment of force produced by the wheel's weight is W*h = = R*cos(30°).
Therefore the moment of force produced by the wheel's weight is W*h = 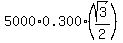 Newtons*meter,
where 0.3 = 0.3 m is the radius of the wheel.
The force F produces the moment Newtons*meter,
where 0.3 = 0.3 m is the radius of the wheel.
The force F produces the moment 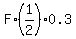 = F*0.15 Newtons*meter.
As you understand (or should understand), the moments of forces, produced by W and F, have opposite directions, and
the equation for the least value of the horizontal force F, through the center of the wheel, required just to turn the wheel
over the corner A of a block is the equality of magnitudes of the two moments of forces (it is the key moment of the solution !)
0.15*F = = F*0.15 Newtons*meter.
As you understand (or should understand), the moments of forces, produced by W and F, have opposite directions, and
the equation for the least value of the horizontal force F, through the center of the wheel, required just to turn the wheel
over the corner A of a block is the equality of magnitudes of the two moments of forces (it is the key moment of the solution !)
0.15*F = 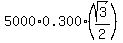 , or
0.15*F = , or
0.15*F = 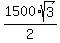 , which implies
F = , which implies
F = 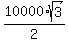 = = 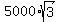 Newtons.
Answer. The least value of the horizontal force F, through the center of the wheel, required just to turn the wheel
over the corner A of a block is Newtons.
Answer. The least value of the horizontal force F, through the center of the wheel, required just to turn the wheel
over the corner A of a block is 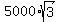 Newtons = 8660 Newtons (approximately).
Regarding the reaction force from the block to the wheel, it is directed along the radius OA from A to O and is equal to Newtons = 8660 Newtons (approximately).
Regarding the reaction force from the block to the wheel, it is directed along the radius OA from A to O and is equal to
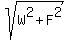 = = 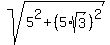 = =  = =  = 10 kilo-Newtons. = 10 kilo-Newtons.
==================
P.S. Until I participate as a tutor in this forum, you can post any standard (or even non-standard) Physics problem.
If it is formulated and presented correctly and professionally, I hope I can solve it
(sometimes even better than what you can find in specialized Physics forums).
Ability to solve practically ANY problem of the School, School+ and even School++ level in Physics and Math
was a necessary condition to pass entrance exams and to be enrolled to the University I graduated from.
Those individuals who solved at the level Math+++, were eligible to be enrolled without the entrance exams.
Later, as a rule, they became professors at universities and some of them became Fields' award laureates in Math . . .
|
|
|