SOLUTION: Are the following lines parallel, perpendicular, or neither? L1 with equation x – 6y = 12 L2 with equation 6x + y = 6

Algebra ->  Points-lines-and-rays -> SOLUTION: Are the following lines parallel, perpendicular, or neither? L1 with equation x – 6y = 12 L2 with equation 6x + y = 6       Log On


   

Question 111294: Are the following lines parallel, perpendicular, or neither?
L1 with equation x – 6y = 12
L2 with equation 6x + y = 6
Found 2 solutions by kmcruz09, MathLover1:
Answer by kmcruz09(38) About Me  (Show Source):
You can put this solution on YOUR website!
The line equations must first be converted to the standard form y+=+mx%2Bb where m is the slope.
So,
x+%96+6y+=+12
x-12=6y
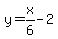
y=x%2F6+-2
y=%281%2F6%29x-2
Then
6x+%2B+y+=+6
y=-6x%2B6
Lines that are perpendicular to each other have negative reciprocal slopes, while lines that are parallel to each other have the same slopes.
Since we already changed the equations to the standard form, we can now take the slope.
For the first line, y=%281%2F6%29x-2, the slope is 1%2F6 as I said before, the literal coefficient of x is the slope in the standard form. Then for the second line, y=-6x%2B6, the slope is -6.
1%2F6 and -6 are negative reciprocals, therefore, the two lines are perpendicular to each other.
graph%28500%2C500%2C-10%2C10%2C-10%2C10%2C%281%2F6%29%2Ax+-2%2C-6x%2B6%29

Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

Solved by pluggable solver: Solve the System of Equations by Graphing



Start with the given system of equations:


1x-6y=12

6x%2By=6





In order to graph these equations, we need to solve for y for each equation.




So let's solve for y on the first equation


1x-6y=12 Start with the given equation



-6y=12-x Subtract +x from both sides



-6y=-x%2B12 Rearrange the equation



y=%28-x%2B12%29%2F%28-6%29 Divide both sides by -6



y=%28-1%2F-6%29x%2B%2812%29%2F%28-6%29 Break up the fraction



y=%281%2F6%29x-2 Reduce



Now lets graph y=%281%2F6%29x-2 (note: if you need help with graphing, check out this solver)



+graph%28+600%2C+600%2C+-10%2C+10%2C+-10%2C+10%2C+%281%2F6%29x-2%29+ Graph of y=%281%2F6%29x-2




So let's solve for y on the second equation


6x%2By=6 Start with the given equation



1y=6-6x Subtract 6+x from both sides



1y=-6x%2B6 Rearrange the equation



y=%28-6x%2B6%29%2F%281%29 Divide both sides by 1



y=%28-6%2F1%29x%2B%286%29%2F%281%29 Break up the fraction



y=-6x%2B6 Reduce





Now lets add the graph of y=-6x%2B6 to our first plot to get:


+graph%28+600%2C+600%2C+-10%2C+10%2C+-10%2C+10%2C+%281%2F6%29x-2%2C-6x%2B6%29+ Graph of y=%281%2F6%29x-2(red) and y=-6x%2B6(green)


From the graph, we can see that the two lines intersect at the point (48%2F37,-66%2F37) (note: you might have to adjust the window to see the intersection)



Since you have m1+=+1%2F6 and m2+=+-6, and perpendicular lines have slope that are negative reciprocals m1+=+-1%2Fm2, then:
m1+=+-1%2Fm2
1%2F6+=+-1%2F-6
1%2F6+=+1%2F6…so, your lines are perpendicular