Question 1111770: A circle is tangent to both the x and y-axis and the equation x+y=8. what are the equations of the circle?
Found 2 solutions by Alan3354, ikleyn:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! A circle is tangent to both the x and y-axis and the equation x+y=8. what are the equations of the circle?
------------------
find the distance from the Origin to the given line.
The center of the circle is the midpoint of the line from the Origin to the given line.
The radius is the x and y of the center (x,y)
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A circle is tangent to both the x and y-axis and the equation x+y=8. what are the equations of the circle?
~~~~~~~~~~~~~~~~~~~~~~~~~
The formulation is, OBVIOUSLY, not exactly correct and, therefore, is not pure Math.
The correct formulation, simultaneously from the Math and the Grammar point of view, is THIS:
A circle is tangent to both the x and y-axis and to the straight line with the equation x+y=8. Find the circles.
Solution
Since the circle is tangent to both the x and y-axis, its center lies at the bisector of the first quadrant angle x = y, and r = x = y.
Now we have two cases (see the Figure below).
Case 1. Small circle inside the triangle.
Coordinates of the center via the radius x = y = r.
Coordinates of the tangent point via the radius  = = 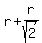 = = 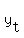 .
Since .
Since  + + 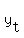 = 8, it gives an equation for "r" = 8, it gives an equation for "r"
 + + 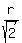 + +  + + 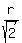 = 8, = 8,
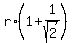 = 4 ====> r = = 4 ====> r = 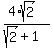 = 2.34 (approx.) = 2.34 (approx.)
 Plot x + y = 8 and two circles.
Case 2. Large circle outside the triangle.
Coordinates of the center via the radius x = y = R.
Coordinates of the tangent point via the radius
Plot x + y = 8 and two circles.
Case 2. Large circle outside the triangle.
Coordinates of the center via the radius x = y = R.
Coordinates of the tangent point via the radius  = = 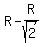 = = 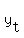 .
Since .
Since  + + 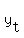 = 8, it gives an equation for "R" = 8, it gives an equation for "R"
 - - 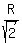 + +  - - 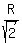 = 8, = 8,
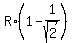 = 4 ====> R = = 4 ====> R =  = 13.66 (approx.)
Answer. Small circle radius r = = 13.66 (approx.)
Answer. Small circle radius r = 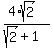 = 2.34 (approx.) and the center x = y = r. The equation is = 2.34 (approx.) and the center x = y = r. The equation is 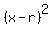 + + 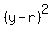 = =  .
Large circle radius R = .
Large circle radius R =  = 13.66 (approx.) and the center x = y = R. The equation is = 13.66 (approx.) and the center x = y = R. The equation is 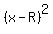 + + 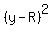 = = 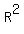 . .
Solved.
|
|
|