|
Question 1106163: vt is an angle bisector of angle svu. If sv=9,vu=20,su=27, find st
Answer by ikleyn(52800)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In any triangle, the angle bisector divides the side to which it is drawn, in two segments proportional to the ratio
of two other sides of a triangle.
For this theorem and its proof, see the lesson
On what segments the angle bisector divides the side of a triangle
in this site.
Using this theorem for the triangle SVU, you get the proportion
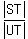 = = 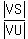 , or , or 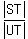 = = 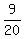 .
The second equation is |ST| + |TU| = 27.
Introducing for breavity x = |ST|, y = |TU|, you have this system of 2 equations
20x - 9y = 0, (1)
x + y = 27. (2)
To solve it, use the Elimination method. For it, multiply eq(2) by 9 (both sides). Keep eq(1) as is. You will get
20x - 9y = 0, (1)
9x + 9y = 243. (2)
Next add equations (1) and (2). You will get
29x = 243.
Hence, x = |ST| = .
The second equation is |ST| + |TU| = 27.
Introducing for breavity x = |ST|, y = |TU|, you have this system of 2 equations
20x - 9y = 0, (1)
x + y = 27. (2)
To solve it, use the Elimination method. For it, multiply eq(2) by 9 (both sides). Keep eq(1) as is. You will get
20x - 9y = 0, (1)
9x + 9y = 243. (2)
Next add equations (1) and (2). You will get
29x = 243.
Hence, x = |ST| = 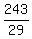 . .
Solved.
|
|
|
| |