Question 1104881: In the figure given below, triangle BAC is inscribed in a semi circle with BC = 73. Semi circles are constructed outside the triangle, with diameter AB = 48 and AC = 55. Find the area of the shaded region inside the two smaller semi circles but outside the larger circle.
http://www.smartlearning.in/new_stsquestion.php?QuestionID=73640&page=1
(please disregard the measurements given in the figure (3 cm and 4 cm) and follow whats stated on the word problem above)
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! You could calculate the shaded area as
the sum of the areas of the two small semicircles,
minus the ate of the large semicircle,
plus the area of the triangle.
The area of the triangle is

because AB and AC are perpendicular,
so we can take one as the base of the triangle,
and the other one would be the height.
We could calculate the areas of the semicircles,
but we do not need to, because we know ABC is a right triangle.
The Pythagorean theorem says that the sum of
the areas of the squares built on the legs of a right triangle
are equal to the area of the square built on the hypotenuse.
It works for semicircles too,
so as you add the areas of the two smaller semicircles,
you get the area of the large one,
and when you subtract it you get zero,
Just before you add the area of the triangle.
In the end, the shaded area is equal to the area of the triangle:
 area units. area units.
If you have to show your work,
and the teacher insists on calculating the area of the semicircles,
the area of a circle is  . .
So, the area of a semicircle is  . .
For the small semicircles the areas are
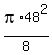 and and 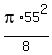 . .
For the large semicircles, the area is
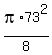 . .
The area of the shaded region is

Of course,  , because ABC is a right triangle. , because ABC is a right triangle.
|
|
|