Question 1101923: Three curtain rods, viewed from a sideways view, each have a diameter 3 cm, and are bound together by a band. The curtain rods (circles) are placed so there are two on the bottom and one on top of those two, in the middle, and the three resemble a triangle). The band goes around the three rods, but does not follow the shapes of the circles perfectly. The band becomes "taut" when it is not touching any part of the circles. Find the length of the band, in cm.
Found 2 solutions by ikleyn, KMST:
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
.
Obviously, the centers of the rods (in the section) form equilateral triangle with the side length of 3 cm. (3 cm = 1.5 cm + 1.5 cm).
So, add 3 + 3 + 3 = 9 centimeters for the length of the 3 linear elements of the band.
Then add to it three times the length of the arc of the circle of the radius 1.5 cm and the central angle of 120 degrees.
So, the final answer is 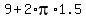 = = 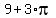 centimeters. centimeters.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here is the drawing of the cross section of the rods bundle to go with ikleyn's solution:

The green triangle connects the centers of the
The red line segments represent the portions of the band not in contact with the circles.
The end of those red segments are at  of the center of one of the circles, of the center of one of the circles,
That distance between (red) line and circle center is measured along the blue lines,
perpendicular to the red lines, of course.
That makes the green=blue-red quadrilateral a rectangle:
two congruent blue opposite sides make a parallelogram,
and a parallelogram with two right angles is a rectangle.
So, the green and te red segments are all conguent, all 3 cm long.
Of the  of central angle (and circumference) around each circle, of central angle (and circumference) around each circle,
 is covered by is covered by
one angle of the triangle,
one angle of a rectangle, and
one angle of another rectangle.
Along the remaining  degrees of its circumference, degrees of its circumference,
each circle is in contact with the bandwrapped around the rod bundle.
|
|
|