Question 1091873: Find 2 equation of a circle that touch the line y=-x+9, the positive y-axis, and positive x-axis
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find 2  equations of a circle that touch the line y=-x+9, the positive y-axis, and positive x-axis. equations of a circle that touch the line y=-x+9, the positive y-axis, and positive x-axis.
~~~~~~~~~~~~~~~~~~~~~~~
1. Since the circle touches the positive y-axis and positive x-axis, its center lies in the angle bisector of the angle
concluded between the axes x and y.
In other words, the center lies in the straight line y = x.
2. There are two such circles in the Quadrant I.
The smaller circle lies inside the right angled triangle formed by the coordinate x- and y-axes and the straight line y = -x + 9.
It is inscribed circle to this triangle.
The other, the larger circle lies outside this triangle and makes external touching with its hypotenuse.
3. Let us solve the problem for the larger circle first.
From what I said above, it is clear that the point (4.5,4.5) lies in the circle and is the touching point.
Now, if you make a sketch, you will easily get the equation for the radius R of the circle:
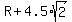 = = 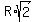 ,
which implies ,
which implies
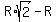 = = 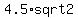 ====> ====>  . .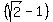 = = 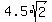 ====> R = ====> R = 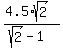 = = 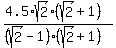 = = 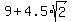 .
Thus the coordinates of the center are (x,y) = (R,R) and the radius is R = .
Thus the coordinates of the center are (x,y) = (R,R) and the radius is R = 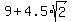 = 15.364 (approximately) (1)
The equation of the larger circle is = 15.364 (approximately) (1)
The equation of the larger circle is 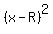 + + 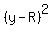 = = 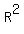 with R expressed in the formula (1).
4. Let us solve the problem for the smaller circle now.
If you make a sketch, you will easily get the equation for the radius r of the smaller circle: with R expressed in the formula (1).
4. Let us solve the problem for the smaller circle now.
If you make a sketch, you will easily get the equation for the radius r of the smaller circle:
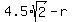 = = 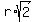 ,
which implies ,
which implies
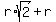 = = 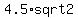 ====> ====>  . .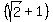 = = 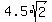 ====> r = ====> r = 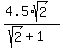 = =  = = 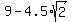 .
Thus the coordinates of the center are (x,y) = (r,r) and the radius is r = .
Thus the coordinates of the center are (x,y) = (r,r) and the radius is r = 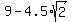 = 2.636 (approximately) (2)
The equation of the smaller circle is = 2.636 (approximately) (2)
The equation of the smaller circle is 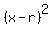 + + 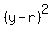 = =  with r expressed by the formula (2). with r expressed by the formula (2).
|
|
|