Question 1088506: please help me solve this problem " Find the equation of the circle inscribed in a triangle, if the triangle has its sides on the lines ; x-y-3=0 , x+y-11=0 , and 7x+y-5=0.
Answer by ikleyn(52817)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
please help me solve this problem:
Find the equation of the circle inscribed in a triangle, if the triangle has its sides on the lines ; x-y-3=0 , x+y-11=0 , and 7x+y-5=0.
~~~~~~~~~~~~~~~~~~~~
The equations of lines are
x - y = 3, (1)
x + y = 11, (2)
7x + y = 5. (3)
1. Notice that the lines (1) and (2) are perpendicular. So the triangle is right-angled.
2. The intersection point of lines (1) and (2) is C = (7,4) (you can find it mentally by adding equations (1) and (2) ).
It is the right-angle vertex.
The intersection point of lines (1) and (3) is A = (1,-2) (you can find it mentally by adding equations (1) and (3) ).
The intersection point of lines (2) and (3) is B = (-1,12) (you can find it mentally by subtracting equations (2) from equation (3) ).
3. The side CA is the vector (-6,-6) of the length  . It is the leg "b" of the triangle.
The side CB is the vector (-8,8) of the length . It is the leg "b" of the triangle.
The side CB is the vector (-8,8) of the length  . It is the leg "a" of the triangle.
The side AB is the vector (-2,14) of the length . It is the leg "a" of the triangle.
The side AB is the vector (-2,14) of the length  . It is the hypotenuse "c" of the triangle.
(classic 3-4-5 right-angled triangle).
4. It is well known fact that the radius of a right-angled triangle with the legs "a" and "b" and the hypotenuse "c" is equal to . It is the hypotenuse "c" of the triangle.
(classic 3-4-5 right-angled triangle).
4. It is well known fact that the radius of a right-angled triangle with the legs "a" and "b" and the hypotenuse "c" is equal to 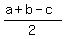 ,
which is in this case ,
which is in this case 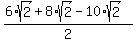 = =  .
5. The center of the circle lies on the angle bisector of the right angle at the vertex C.
This angle bisector is the horizontal line y = 4.
6. The last thing to find is the x-coordinate of the center of the inscribed circle.
This x-coordinate is equal to 7 - .
5. The center of the circle lies on the angle bisector of the right angle at the vertex C.
This angle bisector is the horizontal line y = 4.
6. The last thing to find is the x-coordinate of the center of the inscribed circle.
This x-coordinate is equal to 7 - 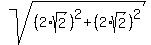 = 7 - = 7 - 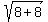 = 7 - = 7 - 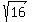 = 7 - 4 = 3.
7. Now we have everything to write the equation of the inscribed circle. It is = 7 - 4 = 3.
7. Now we have everything to write the equation of the inscribed circle. It is
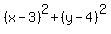 = 8. (8 = = 8. (8 =  = = 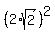 ).
The center is at (3,4); the radius is ).
The center is at (3,4); the radius is  . .
Solved.

|
|
|