Question 1085256: Chord PQ is perpendicular bisector of radius OA of a circle with center O (A is a point on the edge of the circle). If the length of the arc PAQ = 2pie/3. What is the length of the chord PQ?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here is a sketch, with the midpoint of OA labeled as R:
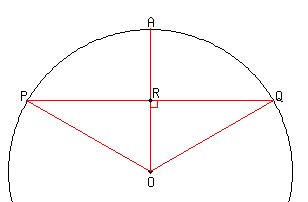 Take a good look at right triangle OQR. Take a good look at right triangle OQR.
The lengths  are the radius, are the radius,  , of the circle. , of the circle.
 is half of that radius. is half of that radius.
That tells you that the short leg of right triangle OQR is half the hypotenuse.
It means that
 (from applying the Pythagorean theorem). (from applying the Pythagorean theorem).
It also means (considering trigonometric ratios for the angles of OQR) that
OQR is a 30-60-90 triangle, with a  angle angle  at O, at O,
which makes angle 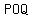 and arc and arc 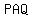 measure measure  , ,
or  of the whole circle. of the whole circle.
If  is the length of arc is the length of arc 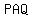 , ,
then  is is  , the length of the circumference. , the length of the circumference.
Then,  , ,  , and , and  . .
|
|
|