SOLUTION: Triangle ABC has vertices A(-2, -3), B(2, 5), and C(6, -7). Find the circumcentre and the centroid.

Let the equation of the circle be



Substituting each of the points, we have this system
of three equations:


 
Subtracting the first two equations





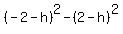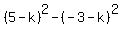Factoring both sides as the difference of squares:







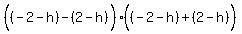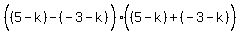
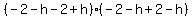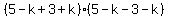
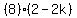Divide both sides by 8

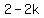  <--equation A 

--------------------------------------

Subtracting the second and third equations





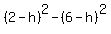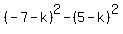Factoring both sides as the difference of squares:







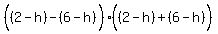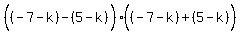
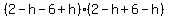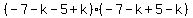
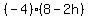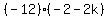Divide both sides by -4





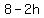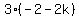
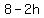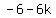Divide both sides by 2





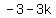
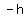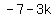
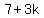  <--equation B

---------------------------------

Setting the expressions for h equal in equations A and B:





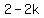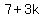
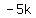
Substituting in equation B





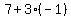
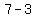
So the circumcenter is (h,k) = (4,-1)

=========================================
=========================================


The centroid is the point where the three medians intersect.
So we will find the equations of two medians and then solve 
the system of equations to find their point of intersection
which will be the centroid.

First we find the midpoint of AB
 


 <--midpoint of AB
We will label that midpoint D

Next we draw the median CD from the vertex C(6,-7)
to the midpoint D(0,1) of the opposite side AB:



Next we find the equation of that line. 

So we find the slope (gradient) of median CD




  <-- slope of CD

Then we use the point-slope formula:



  <-- equation of CD 

---------------------

Now we find the equation of one of the other two medians,
say the median from A to BC 

We find the midpoint of BC
 


 <--midpoint of BC
We will label that midpoint E(4,-1).

[Notice that E(4,-1) just happens to be the circumcenter, the center
of the circle in the first part, which means that BC was a diameter
of the circumscribing circle in the first part.  But that is 
irrelevant to this part, just interesting.]

So we draw the median AE from the vertex A(-2,-3)
to the midpoint E(4,-1) of the opposite side AB:



Next we find the equation of the median AE. 

So we find the slope (gradient) of median AE




  <-- slope of median AE

Then we use the point-slope formula:






  <-- equation of AE 

To find the centroid we solve this system of
equations to find the point where those two
medians intersect:



We set the two expressions for y equal:



Multiply through by 3







Substitute in







So the centroid (the point where the two (green)
medians intersect is  

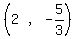Edwin