Question 1082466: A circle has a center (0,9) and radius 9. A second circle with radius 4, touches the first circe and the x-axis
a) If the second circle lies in the first quadrant, find its equation
b) Find the possible equations for the second circle if it does not lie in the first quadrant
Answer by ikleyn(52923)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A circle has a center (0,9) and radius 9. A second circle with radius 4, touches the first circe and the x-axis
a) If the second circle lies in the first quadrant, find its equation
b) Find the possible equations for the second circle if it does not lie in the first quadrant
~~~~~~~~~~~~~~~~
a)
0. Make a sketch to follow my arguments.
Let A and B be the centers of the circles (A lies at y-axis).
Connect the points A and B by the straight segment.
From the point B draw the horizontal straigh line till the intersection with y-axis.
Let C be the intersection point with y-axis.
1. Then you have a right-angled triangle ABC.
The length of AB is |AB| = 9 + 4 = 13 units. (Since "a second circle with radius 4 touches the first circle"
The length of AC is |AC| = 9-4 = 5 units. (Since "a second circle with radius 4, touches the x-axis")
2. Hence, the length of BC is |BC| = 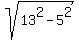 = 12 units.
3. Thus the center of the second circle is at the point (x,y) = (12,4).
4. Now, the equation of the second circle is = 12 units.
3. Thus the center of the second circle is at the point (x,y) = (12,4).
4. Now, the equation of the second circle is
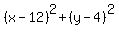 = =  , or, which is the same, , or, which is the same, 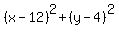 = 16. = 16.
Solved.
|
|
|