|
Question 1079874: Find the point of intersection of  and 3x-5y+2=0. May I request for a step by step procedure on solving so I can study it further.
Found 2 solutions by KMST, rothauserc:
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! I see three ways to tackle this problem:
1) ONE WAY:
Solve  for x or for y,
and substitute into the other equation.
I don't even want to try that.
2) ANOTHER WAY:
Figure out what the graphs of those equations are,
and figure out a smarter way to the solution.
 represents a straight line,
with intercepts (-2/3,0) and (0,2/5) .
 <--> 
represents a circle centered at (-2,6)
with radius  .
3) SMARTEST WAY:
Do as in 2), but figure the smartest way.
Way # 2:
I would solve for x
-->  -->  ,
and would substitute it into
 to get
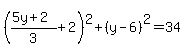
That has only one solution:  ,
and substituting into  we find
 , so  .
Way #3:
Maybe the fact that it says "the point"
and not "the points" is a clue.
Once you realize that the equations graph as a line and a circle,
You know that the intersection points could be 2, 1, or none.
You can verify it is one point, as the problem hints,
by using the distance to a line formula
to verify the center of the circle is
at distance from the line:
For a point (x,y) and a line  .
 .
In this case, the distance from circle center (-2,6)
to is
The line is tangent to the circle,
and the radius at the one point where they touch
is perpendicular to the line.
The line <-->
has a slope of  ,
so a perpendicular line has a slope of  .
The radius at the intersection point
is a line with that slope going through circle center (-2,6) ,
So its equation is
The point of tangent of line and circle
Is the intersection of that radius with line .
, and substituting into ,
we find  .
So the solution is  ,
and the intersection point is (1,1) .
Answer by rothauserc(4718)  (Show Source):
You can put this solution on YOUR website! Solve 3x-5y+2=0 for y
:
5y = 3x + 2
1) y = 3x/5 + 2/5
:
rewrite x^2 + y^2 + 4x - 12y + 6 = 0 into the standard form for a circle by completing the squares
:
x^2+4x+4 + y^2-12y+36 = -6 +4 +36
2) (x+2)^2 + (y-6)^2 = 34
:
use equation 1 and substitute for y in equation 2
:
(x+2)^2 + (3x/5 + 2/5 - 6)^2 = 34
x^2+4x+4 + (9x^2/25) -(168x/25) +(784/25) = 34
:
multiply both sides of = by 25
:
25x^2 +100x +100 + 9x^2 -168x + 784 = 850
:
34x^2 - 68x +34 = 0
:
x^2 - 2x +1 = 0
:
(x-1)^2 = 0
:
x-1 = 0
x = 1
substitute the value for x in equation 1 to get the corresponding value for y
:
y = (3 * 1 / 5) + (2 / 5) = 5/5 = 1
:
***************************************************************
the point of intersection is (1, 1)
:
Note that this is a tangent point with the circle and the line
:
to check the answer substitute for x and y in equation
:
x^2 + y^2 + 4x - 12y + 6 = 0
:
(1)^2 + (1)^2 + (4 * 1) - (12 * 1) + 6 = 0
:
our answer checks
***************************************************************
:
|
|
|
| |
