SOLUTION: Find the equation of the circle that passes through the origin and (2,4); tangent to the line 3x - 2y = 12.

Algebra ->  Circles -> SOLUTION: Find the equation of the circle that passes through the origin and (2,4); tangent to the line 3x - 2y = 12.      Log On


   

Question 1079015: Find the equation of the circle that passes through the origin and (2,4); tangent to the line 3x - 2y = 12.
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39623) About Me  (Show Source):
You can put this solution on YOUR website!
MISTAKE In READING-
Mistook (2,4) as Center of Circle-

The radius tangent to the given line is perpendicular to the given line, and is on the line y-4=-%282%2F3%29%28x-2%29. Find their intersection point; or at which point does y-4=-%282%2F3%29%28x-2%29 intersect with 3x-2y=12? Then, what is the distance from this point to (2,4)? From this length, determine r%5E2.

Finish filling-in cross%28%28x-2%29%5E2%2B%28y-4%29%5E2=r%5E2%29.

Answer by ikleyn(52834) About Me  (Show Source):
You can put this solution on YOUR website!
.
Find the equation of the circle that passes through the origin and (2,4); tangent to the line 3x - 2y = 12.
~~~~~~~~~~~~~~~~~~~~~~~ 

According to the condition, the circle passes through the points (0,0) and (2,4).
Therefore, its center lies on the perpendicular bisector of the segment connecting these points.


     Now, the idea on how to solve the problem is to find the point on the perpendicular bisector EQUIDISTANT from the given points 
          AND from the given straight line.


The midpoint between (0,0) and (2,4) is the point (1,2).

The slope of the segment connecting (0,0) and (2,4) is 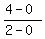%284-0%29%2F%282-0%29 = 2.
Hence, the slope of the perpendicular bisector is -1%2F2.

Thus the equation of the perpendicular bisector passing through (1,2) is

y - 2 = 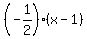%28-1%2F2%29%2A%28x-1%29


From the other side, the distance from the point (x,y) to the given straight line 3x - 2y = 12 is equal to

d = 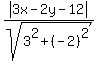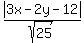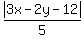abs%283x+-+2y+-12%29%2Fsqrt%283%5E2%2B%28-2%29%5E2%29 = abs%283x+-+2y+-12%29%2Fsqrt%2825%29 = abs%283x+-+2y+-12%29%2F5,

according to the lesson The distance from a point to a straight line in a coordinate plane in this site.


Therefore, the center of the circle lies on the straight line

y - 2 = 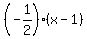%28-1%2F2%29%2A%28x-1%29

and is equidistant from the point (0,0) and the straight line 3x-2y - 12 = 0, which means

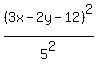x%5E2+%2B+y%5E2 = %283x+-+2y+-12%29%5E2%2F5%5E2.


Thus the problem is reduced to solving this system of equations

y - 2 = 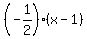%28-1%2F2%29%2A%28x-1%29        (1)     and

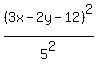x%5E2+%2B+y%5E2 = %283x+-+2y+-12%29%5E2%2F5%5E2.     (2)


The setup is done. The rest is just technique.

Writing of "josgarithmetic" on this problem is wrong and irrelevant.