SOLUTION: Find the equation of the circle that passes through (1,2) and (3,4); centre on 3x + y - 13 = 0.

The locus of the points equidistant from two given points is the perpendicular bisector to the segment connecting these points.


So, you need to construct the perpendicular bisector to the segment connecting (1,2) and (3,4), and then 
find its intersection with the given straight line.


The midpoint between the two given points is (2,3).


The segment connecting (1,2) and (3,4) has the slope 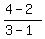 = 1.

Hence, the perpendicular line (perpendicular bisector) has the slope -1.


The line with the slope -1 passing through the point (2,3) has the equation 

y - 3 = (-1)*(x-2),   or

y = -x + 5.


The intersection of the straight lines

3x + y = 13     (1)   (the given line)   and
y = -x + 5      (2)   (the perpendicular bisector)

is (solve the system by substitution) the point (x,y) = (4,1)

So, the center of the circle is the point (4,1).


The radius of the circle is the distance from the point (4,1) to the point (3,4):

r =  =  = .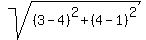


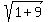Therefore, the equation of this circle is 

 = 10.