Question 1074904: An ellipse and a hyperbola have the same foci, $A$ and $B$, and intersect at four points. The ellipse has major axis 50, and minor axis 40. The hyperbola has conjugate axis of length 20. Let $P$ be a point on both the hyperbola and ellipse. What is $PA \cdot PB$?
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! If P is a point in an ellipse with foci A and B, and major axis 50,
by the definition of ellipse,
PA+PB=50.
If the minor axis of that ellipse is 40,
them the semimajor and senior acrs are respectively
a=25 and b=20.
That makes the focal distance
c=15.
For a hyperbola, the focal distance,
the distance between the vertices (the transverse axis),
and the conjugate axis are related by
 , where c is the focal distance,
2b is the conjugate axis, and
2a is the transverse axis.
So for this hyperbola, 2b=20, so b=10,
and c=15, so
 .
That makes 2a=10.
That is the distance between the vertices.
If P is a point in a hyperbola with foci A and B,
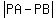 = distance between the vertices.
So, for this hyperbola
 ---> 
We knew for the ellipse that
PA+PB=50 --->  .
Since  ,
 and 
|
|
|
