Question 1073955: six congruents circular poles, each with a radius of 3 inches, are bound together by a rope wrapped around the circles two times. find the length of the rope. the circles are tangent to eachother
Found 3 solutions by CubeyThePenguin, ikleyn, greenestamps:
Answer by CubeyThePenguin(3113)   (Show Source): (Show Source):
Answer by ikleyn(52799)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
six congruent circular poles, each with a radius of 3 inches, are bound together by a rope
wrapped around the circles two times. find the length of the rope. the circles are tangent to each other
~~~~~~~~~~~~~~~~~
I imagine 6 (six, SIX) poles, arranged and attached in this way that they form an equilateral triangle in section.
Then the rope has three lineare segments along each side of this equilateral triangle;
each linear segment has the length equal to 4r = 4*3 = 12 inches.
Next, there are 3 arcs of 120 degrees each, contributing 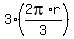 = = 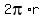 to the rope length.
Having the rope wrapped two times around the circles bounded together, gives the length of such rope of
2 * [ (3*4r) + to the rope length.
Having the rope wrapped two times around the circles bounded together, gives the length of such rope of
2 * [ (3*4r) + 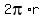 ] = 2*(3*4*3) + ] = 2*(3*4*3) + 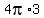 = 72 + 4*3.14*3 = 109.68 inches (approximately. ANSWER
Thus you have both the formula and the value. = 72 + 4*3.14*3 = 109.68 inches (approximately. ANSWER
Thus you have both the formula and the value.
Solved.
----------
Notice that the plot and the solution of the other tutor is irrelevant to the considered configuration.
////////////
Added after reading the post by @greenestamps.
My arrangement of 6 poles is ONVIOUS:
imagine first 3 poles lying next to each other on horizontal plane.
imagine 2 poles in the next (second) row above the first one
finally, imagine the last, third row over the two in the second row.
Their centers form equilateral triangle, and this configuration is stable.
Actually, this configuration is FIRST than come to the mind when speaking about it . . .
So, my solution is perfect, independently of what @greenestamps think or may think about it.
If somebody has difficulties in understanding such simple things, I may advise to look into the picture in the lesson
- Word problems on arithmetic progressions
in this site.
This picture shows placement of tubes, but you may think that you see poles instead of tubes.
Now think that you see only six tubes/poles placed in three rows.
To explain such simple things is the same pleasure as to chew a resina in the mouth,
but for especially dumb persons I am ready to spend my time for it.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
With the problem as stated, it is only guesswork to try to find the solution, because we don't know how the 6 circular poles would be arranged.
With SEVEN circular poles, the solution could be as shown by one of the tutors who have supplied responses to the problem. The 7th pole in the center makes a predictable and stable arrangement of the other 6 poles.
The other tutor supplied a response assuming the 6 poles are bound together in an arrangement that forms an equilateral triangle. That arrangement of the poles allows for a solution to the problem; and her solution for that arrangement is correct.
However, that arrangement of the poles is not stable. 6 poles bound together as tightly as possible with a flexible rope would not form an equilateral triangle.
The actual solution to the problem would require some complicated analysis of the physics involved and what the arrangement of the 6 poles would be.
So we can't know what the correct solution to the problem is.
|
|
|